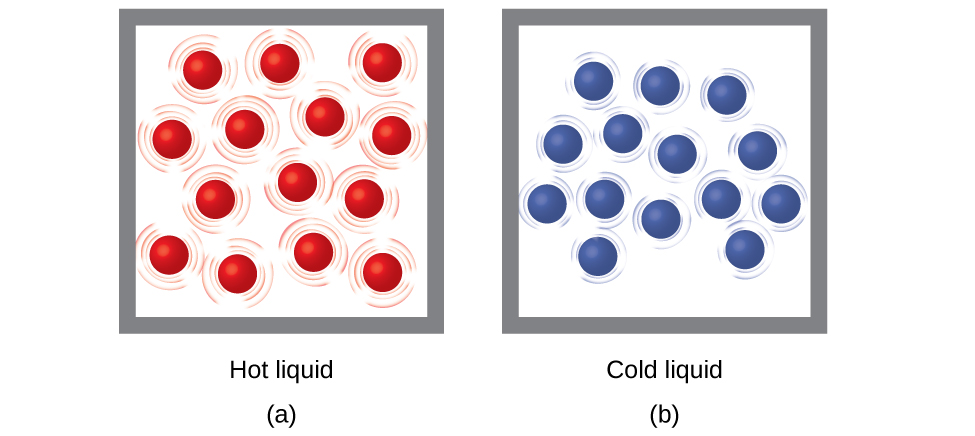
Thermal energy is the kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower average KE, and we say that the object is “cold”. Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.
Click on this interactive simulation to view the effects of temperature on molecular motion.
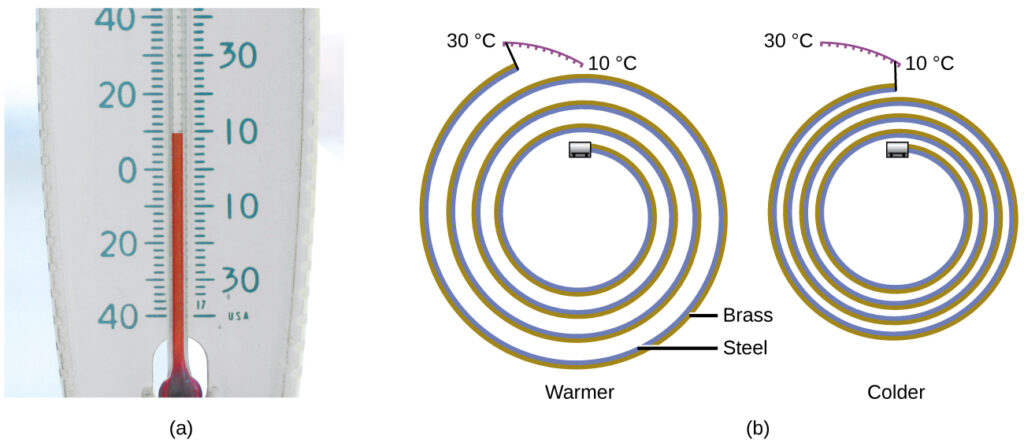
Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in the figure below. The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.

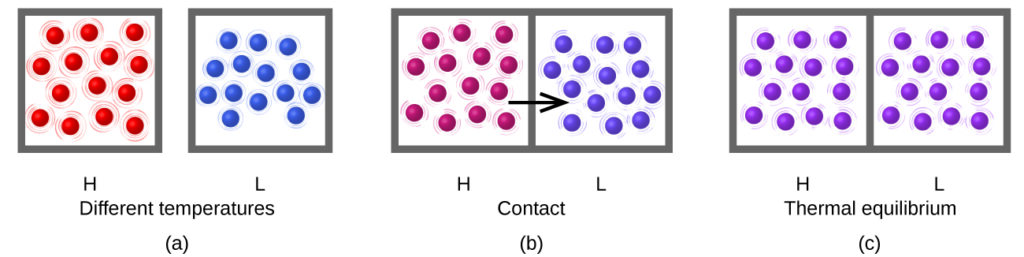
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Heat flow will continue until the two substances are at the same temperature (see figure below).
Use the PhET simulation below to explore energy forms and changes. Visit the Energy Systems tab to create combinations of energy sources, transformation methods, and outputs. Click on Energy Symbols to visualize the transfer of energy.
Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame in the image below. A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt like ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold.

Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 meter. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m2/s2, which is also called 1 newton–meter. A kilojoule (kJ) is 1000 joules. To standardize its definition, 1 calorie has been set to equal 4.184 joules.
We now introduce two concepts useful in describing heat flow and temperature change. The heat capacity (C) of a body of matter is the quantity of heat (q) it absorbs or releases when it experiences a temperature change (ΔT) of 1 degree Celsius (or equivalently, 1 kelvin): $$C=\frac{q}{ΔT}$$
Heat capacity is determined by both the type and amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.
For example, consider the heat capacities of two cast iron frying pans. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. The heat capacity of the small cast iron frying pan is found by observing that it takes 18,150 J of energy to raise the temperature of the pan by 50.0 °C:
$$C_{small pan}=\frac{18,140\;J}{50.0°C}=363\;J/°C$$
The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:
$$C_{large pan}=\frac{90,700\;J}{50.0°C}=1814\;J/°C$$
The specific heat capacity (c) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):
$$c=\frac{q}{mΔT}$$
Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore:
$$c_{iron}=\frac{18 140\;J}{(808\;g)(50.0°C)}=0.449\;J/g °C$$
The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:
$$c_{iron}=\frac{90 700\;J}{(4040\;g)(50.0°C)}=0.449\;J/g °C$$
Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/mol °C.

water has a relatively high specific heat (about 4.2 J/g °C for the liquid and 2.09 J/g °C for the solid)); most metals have much lower specific heats (usually less than 1 J/g °C). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this chapter. Specific heats of some common substances are listed in the table below.
Specific Heats of Common Substances at 25 °C and 1 bar
| Substance | Symbol (state) | Specific Heat (J/g °C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| air | 1.007 | |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:
$$q=(specific\;heat)×(mass\;of\;substance)×(temperature\;change)$$
$$q=c×m×ΔT=c×m×(T_{final}−T_{initial})$$
In this equation, c is the specific heat of the substance, m is its mass, and ΔT (which is read “delta T”) is the temperature change, Tfinal − Tinitial. If a substance gains thermal energy, its temperature increases, its final temperature is higher than its initial temperature, Tfinal − Tinitial has a positive value, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, the final temperature is lower than the initial temperature, Tfinal − Tinitial has a negative value, and the value of q is negative.
Measuring Heat
A flask containing $8×10^2\;g$ of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?
Solution
To answer this question, consider these factors:
- the specific heat of the substance being heated (in this case, water)
- the amount of substance being heated (in this case, 8.0 × 102 g)
- the magnitude of the temperature change (in this case, from 21 °C to 85 °C).
The specific heat of water is 4.184 J/g °C, so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 8.0 × 102 g of water by 1 °C. Finally, we observe that since 4.184 J are required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using the equation:
$$q=c×m×ΔT\\ =c×m×(T_{final}−T_{initial})$$
$$=(4.184J/g°C)×(8.0\times 102g)×(85−21)°C \\ =(4.184J/g°C)×(8.0\times 102g)×(64)°C \\ =210,000 J(=2.1\times 10^2 \;kJ)$$
Because the temperature increased, the water absorbed heat and q is positive.
Check Your Learning
How much heat, in joules, must be added to a 502 g iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.449 J/g °C.
Answer:
5.07 × 104 J
Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.
Determining Other Quantities
A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4 °C to 43.6 °C. Determine the specific heat of this metal (which might provide a clue to its identity).
Solution:
Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using the relationship: q=c×m×ΔT=c×m×(Tfinal−Tinitial)q=c×m×ΔT=c×m×(Tfinal−Tinitial)
Substituting the known values: $$6640 J=c×(348 g)\times (43.6−22.4)°C$$
Solving: $$c=6640 J(348 g)\times (21.2°C)=0.900J/g °C $$
Comparing this value with the values in the table above, this value matches the specific heat of aluminum, which suggests that the unknown metal may be aluminum.
Check Your Learning
A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity.
Answer:
c = 0.451 J/g °C; the metal is likely to be iron.
Solar Thermal Energy Power Plants
The sunlight that reaches the earth contains thousands of times more energy than we presently capture. Solar thermal systems provide one possible solution to the problem of converting energy from the sun into energy we can use. Large-scale solar thermal plants have different design specifics, but all concentrate sunlight to heat some substance; the heat “stored” in that substance is then converted into electricity.
The Solana Generating Station in Arizona’s Sonora Desert produces 280 megawatts of electrical power. It uses parabolic mirrors that focus sunlight on pipes filled with a heat transfer fluid (HTF) ([link]). The HTF then does two things: It turns water into steam, which spins turbines, which in turn produces electricity, and it melts and heats a mixture of salts, which functions as a thermal energy storage system. After the sun goes down, the molten salt mixture can then release enough of its stored heat to produce steam to run the turbines for 6 hours. Molten salts are used because they possess a number of beneficial properties, including high heat capacities and thermal conductivities.
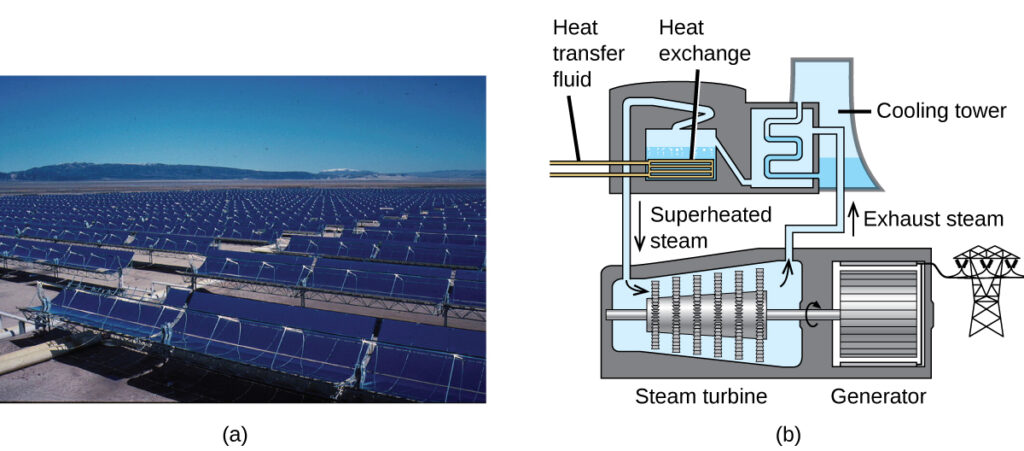
The 377-megawatt Ivanpah Solar Generating System, located in the Mojave Desert in California, is the largest solar thermal power plant in the world ([link]). Its 170,000 mirrors focus huge amounts of sunlight on three water-filled towers, producing steam at over 538 °C that drives electricity-producing turbines. It produces enough energy to power 140,000 homes. Water is used as the working fluid because of its large heat capacity and heat of vaporization.
