The Atomic Mass Unit (amu) is a unit derived from the structure of the atom: one amu (atomic mass unit) is exactly 1/12th of the mass of one carbon-12 atom: 1 amu = 1.6605×10−24 g
Because each proton and each neutron in the atom’s nucleus contribute approximately one amu to the mass of an atom, and each electron contributes far less, the atomic mass of a single atom is approximately equal to its mass number (a whole number). However, the average masses of atoms of most elements are not whole numbers because most elements exist naturally as mixtures of two or more isotopes.
Determining Average Atomic Masses
The mass of an element shown in a periodic table or listed in a table of atomic masses is a weighted, average mass of all the isotopes present in a naturally occurring sample of that element. This is equal to the sum of each individual isotope’s mass multiplied by its fractional abundance.
$$ \text{average mass} = \sum \text{(fractional abundance × isotopic mass)} $$
For example, the element boron is composed of two isotopes: About 19.9% of all boron atoms are 10B with a mass of 10.0129 amu, and the remaining 80.1% are 11B with a mass of 11.0093 amu. The average atomic mass for boron is calculated to be:
$$ \text{boron average mass} = (0.199 \times 10.0129\; \text{amu}) + (0.801 \times 11.0093\; \text{amu}) \\
= 1.99\; \text{amu}+ 8.82\; \text{amu}\\
= 10.81\; \text{amu}$$
It is important to understand that no single boron atom weighs exactly 10.8 amu; 10.8 amu is the average mass of all boron atoms, and individual boron atoms weigh either approximately 10 amu or 11 amu.
Calculation of Average Atomic Mass
A meteorite found in central Indiana contains traces of the noble gas neon picked up from the solar wind during the meteorite’s trip through the solar system. Analysis of a sample of the gas showed that it consisted of 91.84% 20Ne (mass 19.9924 amu), 0.47% 21Ne (mass 20.9940 amu), and 7.69% 22Ne (mass 21.9914 amu). What is the average mass of the neon in the solar wind?
Solution
| average mass | =$(0.9184×19.9924\;amu)+(0.0047×20.9940\;amu)+(0.0769×21.9914\;amu)$ |
| =$(18.36+0.099+1.69)\;amu$ | |
| =$20.15\;amu$ |
The average mass of a neon atom in the solar wind is 20.15 amu. (The average mass of a terrestrial neon atom is 20.1796 amu. This result demonstrates that we may find slight differences in the natural abundance of isotopes, depending on their origin.)
Check Your Learning
A sample of magnesium is found to contain 78.70% of 24Mg atoms (mass 23.98 amu), 10.13% of 25Mg atoms (mass 24.99 amu), and 11.17% of 26Mg atoms (mass 25.98 amu). Calculate the average mass of a Mg atom.
Answer:
24.31 amu
We can also do variations of this type of calculation, as shown in the next example.
Calculation of Percent Abundance
Naturally occurring chlorine consists of 35Cl (mass 34.96885 amu) and 37Cl (mass 36.96590 amu), with an average mass of 35.453 amu. What is the percent composition of Cl in terms of these two isotopes?
Solution
The average mass of chlorine is the fraction that is 35Cl times the mass of 35Cl plus the fraction that is 37Cl times the mass of 37Cl.
If we let x represent the fraction that is 35Cl, then the fraction that is 37Cl is represented by 1.00 − x.
(The fraction that is 35Cl + the fraction that is 37Cl must add up to 1, so the fraction of 37Cl must equal 1.00 − the fraction of 35Cl.)
Substituting this into the average mass equation, we have:
So solving yields: x = 0.7576, which means that 1.00 − 0.7576 = 0.2424. Therefore, chlorine consists of 75.76% 35Cl and 24.24% 37Cl.
Check Your Learning
Naturally occurring copper consists of 63Cu (mass 62.9296 amu) and 65Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What is the percent composition of Cu in terms of these two isotopes?
Answer:
69.15% Cu-63 and 30.85% Cu-65
Use the simulation below to make mixtures of the main isotopes of the first 18 elements, gain experience with average atomic mass, and check naturally occurring isotope ratios.
Curious as to how the natural abundances of isotopes can be experimentally determined? Click here!
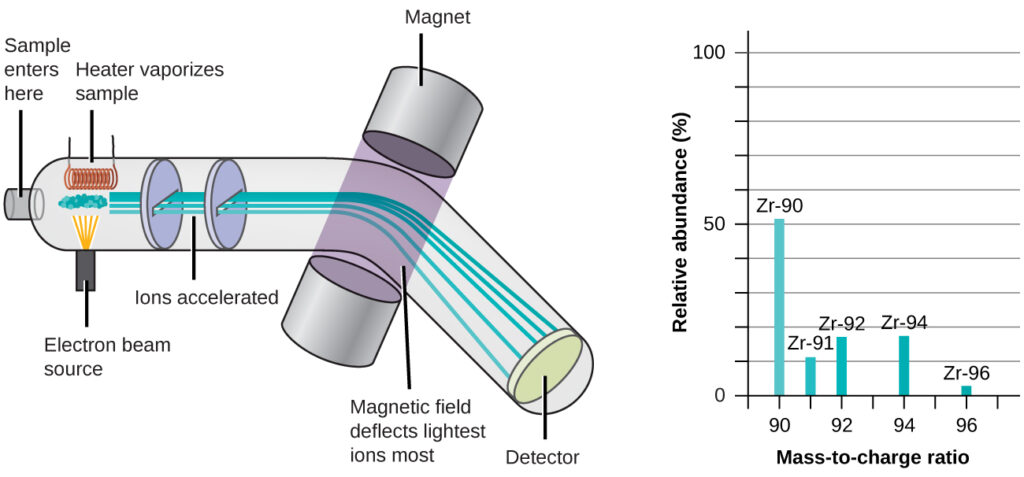
The occurrence and natural abundances of isotopes can be experimentally determined using an instrument called a mass spectrometer. Mass spectrometry (MS) is widely used in chemistry, forensics, medicine, environmental science, and many other fields to analyze and help identify the substances in a sample of material. In a typical mass spectrometer (Figure 2.15), the sample is vaporized and exposed to a high-energy electron beam that causes the sample’s atoms (or molecules) to become electrically charged, typically by losing one or more electrons. These cations then pass through a (variable) electric or magnetic field that deflects each cation’s path to an extent that depends on both its mass and charge (similar to how the path of a large steel ball bearing rolling past a magnet is deflected to a lesser extent that that of a small steel BB). The ions are detected, and a plot of the relative number of ions generated versus their mass-to-charge ratios (a mass spectrum) is made. The height of each vertical feature or peak in a mass spectrum is proportional to the fraction of cations with the specified mass-to-charge ratio. Since its initial use during the development of modern atomic theory, MS has evolved to become a powerful tool for chemical analysis in a wide range of applications.