A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These quantitative relationships are known as the reaction’s stoichiometry, a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this module, the use of balanced chemical equations for various stoichiometric applications is explored.
The general approach to using stoichiometric relationships is similar in concept to the way people go about many common activities. Food preparation, for example, offers an appropriate comparison.
To start, let’s bring back the grilled cheese sandwich example:
2 slices of bread + 1 slice of cheese ⟶ 1 sandwich
If we need to make 6 sandwiches we need:
$$6\,sandwiches\,\times \frac{2\,slices\,of\,bread}{1\,sandwich}=\,12\,slices\,of\,bread$$and
$$6\,sandwiches\,\times \frac{1\,slices\,of\,cheese}{1\,sandwich}=\,6\,slices \,of \,cheese$$The 2:1 ratio of bread to sandwich and the 1:1 ratio of cheese to sandwich are our stoichiometric ratios and they can be used to determine how much of each “reactant” we need in order to make a set amount of our “product” (6 sandwiches in this case). By comparing the coefficients in front of the reactants and products we can determine the stoichiometric ratios and use this ratio to determine how much of each reactant we need to make a certain amount of product.
Let’s move on to a slightly more complex food preparation analogy. A recipe for making eight pancakes calls for 1 cup pancake mix,$\frac{3}{4}$ cup milk, and one egg. The “equation” representing the preparation of pancakes per this recipe is
$$1\,cup\,mix\,+\,\frac{3}{4}cup\,milk\,+\,1\,egg\,⟶\,8\,pancakes$$If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is
$$24\,pancakes\,\times\frac{1\,egg}{8\,pancakes}=\,3\,eggs$$Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product, and so forth. The coefficients in the balanced equation are used to derive stoichiometric factors that permit computation of the desired quantity. To illustrate this idea, consider the production of ammonia by reaction of hydrogen and nitrogen:
N2(g) + 3H2(g) ⟶ 2NH3(g)
This equation shows ammonia molecules are produced from hydrogen molecules in a 2:3 ratio, and stoichiometric factors may be derived using any amount (number) unit:
$$\frac{2\,NH_3\,molecules}{3\,H_2\,molecules}\,or\,\frac{2\,doz\,NH_3\,molecules}{3\,doz\,H_2\,molecules}\,or\,\frac{2\,mol\,NH_3\,molecules}{3\,mol\,H_2\,molecules}$$These stoichiometric factors can be used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Similar factors may be derived for any pair of substances in any chemical equation.
Moles of Reactant Required in a Reaction
How many moles of I2 are required to react with 0.429 mol of Al according to the following equation?
2Al + 3I2 ⟶ 2AlI3

Solution:
Referring to the balanced chemical equation, the stoichiometric factor relating the two substances of interest is: $$\frac{3\,mol\,I_2}{2\,mol\,Al}$$
The molar amount of iodine is derived by multiplying the provided molar amount of aluminum by this factor:

Check Your Learning
Once you have the above correct, you can use this understanding to complete the question:
Number of Product Molecules Generated by a Reaction
How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?
C3H8 + 5O2 ⟶ 3CO2 + 4H2O
Solution
The approach here is the same as for the example above, though the absolute number of molecules is requested, not the number of moles of molecules. This will simply require use of the moles-to-numbers conversion factor, Avogadro’s number.
The balanced equation shows that carbon dioxide is produced from propane in a 3:1 ratio: $\frac{3\,mol\,CO_2}{1\,mol\,C_3H_8}$
Using this stoichiometric factor, the provided molar amount of propane, and Avogadro’s number,

Check Your Learning
How many NH3 molecules are produced by the reaction of 4.0 mol of Ca(OH)2 according to the following equation:
(NH4)2SO4 + Ca(OH)2 ⟶ 2NH3 + CaSO4 + 2H2O
Answer:
4.8 × 1024 NH3 molecules
These examples illustrate the ease with which the amounts of substances involved in a chemical reaction of known stoichiometry may be related. Directly measuring numbers of atoms and molecules is, however, not an easy task, and the practical application of stoichiometry requires that we use the more readily measured property of mass.
Relating Masses of Reactants and Products
What mass of sodium hydroxide, NaOH, would be required to produce 16 g of the antacid milk of magnesia [magnesium hydroxide, Mg(OH)2] by the following reaction?
MgCl2(aq) + 2NaOH(aq) ⟶ Mg(OH)2(s) + 2NaCl(aq)
Solution:
The approach used in the previous examples is likewise used here; that is, we must derive an appropriate stoichiometric factor from the balanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, however, masses (not molar amounts) are provided and requested, so additional steps of the sort learned in the previous chapter are required. The calculations required are outlined in this flowchart:
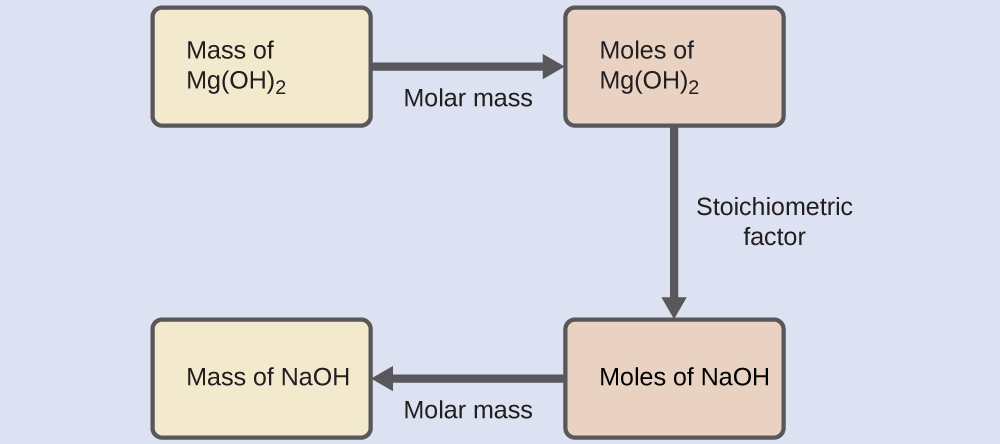
$$16\,\require{enclose}\enclose{horizontalstrike}{g\,Mg(OH)_2}\,×\frac{1\,\enclose{horizontalstrike}{mol\,Mg(OH)_2}}{58.3\,\enclose{horizontalstrike}{g\,Mg(OH)_2}}×\frac{2\,\enclose{horizontalstrike}{mol\,NaOH}}{1\,\enclose{horizontalstrike}{mol\,Mg(OH)_2}}×\frac{40.0\,g\,NaOH}{\enclose{horizontalstrike}{mol\,NaOH}}=\mathbf{\,22\,g\,NaOH}$$
Check Your Learning
What mass of gallium oxide, Ga2O3, can be prepared from 29.0 g of gallium metal? The equation for the reaction is 4Ga + 3O2 ⟶ 2Ga2O3.
Answer
39.0 g
Relating Masses of Reactants
What mass of oxygen gas, O2, from the air is consumed in the combustion of 702 g of octane, C8H18, one of the principal components of gasoline?
2C8H18 + 25O2 ⟶ 16CO2 + 18H2O
Solution
The approach required here is the same, differing only in that the provided and requested masses are both for reactant species.
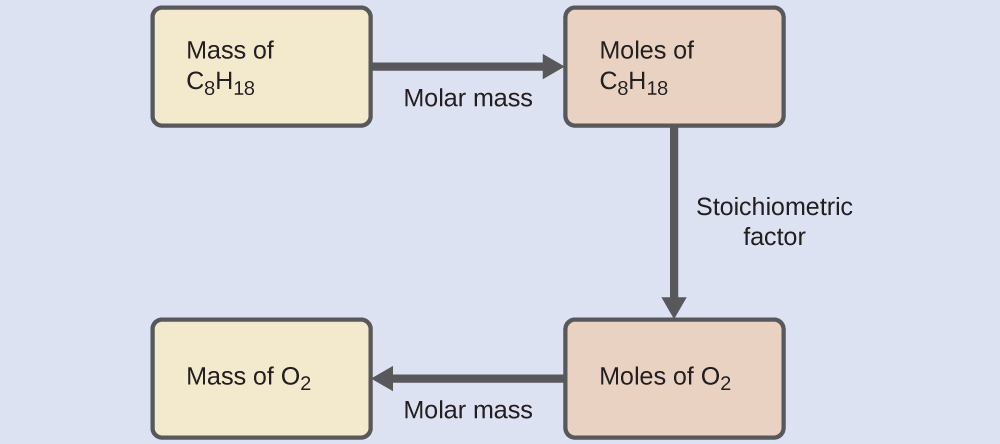
$$702\,\require{enclose}\enclose{horizontalstrike}{g\,C_8H_{18}}\,×\frac{1\,\enclose{horizontalstrike}{mol\,C_8H_{18}}}{114.23\,\enclose{horizontalstrike}{g\,C_8H_{18}}}×\frac{25\,\enclose{horizontalstrike}{mol\,O_2}}{2\,\enclose{horizontalstrike}{mol\,C_8H_{18}}}×\frac{32.00\,g\,O_2}{\enclose{horizontalstrike}{mol\,O_2}}=\mathbf{\,2.46\,×\,10^3\,g\,O_2}$$
Check Your Learning
What mass of CO is required to react with 25.13 g of Fe2O3 according to the equation Fe2O3 + 3CO ⟶ 2Fe + 3CO2?
Answer
13.22 g
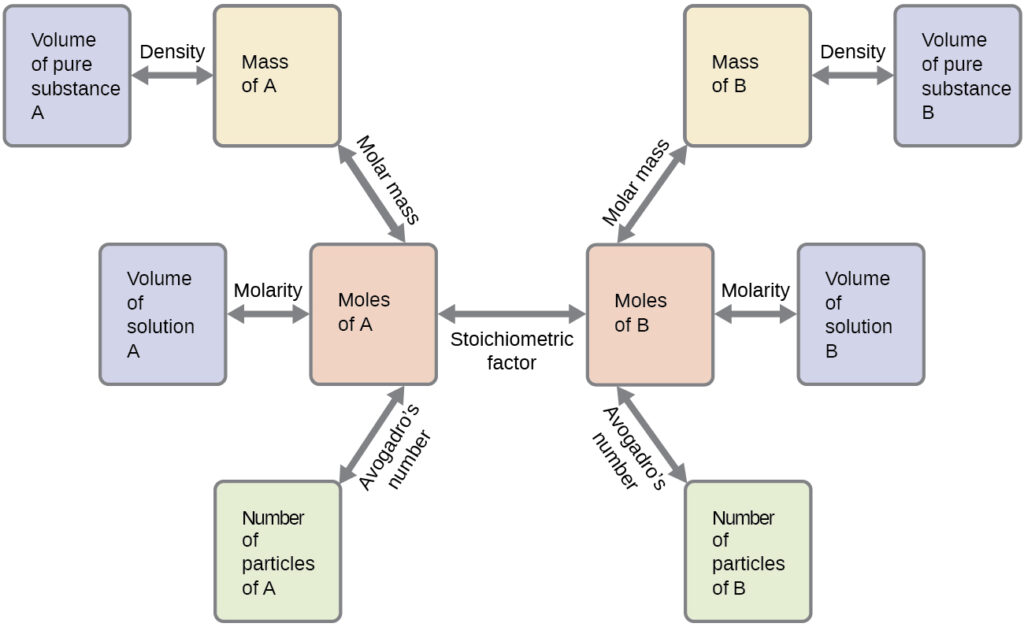
These examples illustrate just a few instances of reaction stoichiometry calculations. Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. The figure below provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.
Airbags: A Gas Producing Reaction
Airbags are a safety feature provided in most automobiles since the 1990s. The effective operation of an airbag requires that it be rapidly inflated with an appropriate amount (volume) of gas when the vehicle is involved in a collision. This requirement is satisfied in many automotive airbag systems through use of explosive chemical reactions, one common choice being the decomposition of sodium azide, NaN3. When sensors in the vehicle detect a collision, an electrical current is passed through a carefully measured amount of NaN3 to initiate its decomposition:
2NaN3(s) ⟶ 3N2(g) + 2Na(s)
This reaction is very rapid, generating gaseous nitrogen that can deploy and fully inflate a typical airbag in a fraction of a second (~0.03–0.1 s). Among many engineering considerations, the amount of sodium azide used must be appropriate for generating enough nitrogen gas to fully inflate the air bag and ensure its proper function. For example, a small mass (~100 g) of NaN3 will generate approximately 50 L of N2.
