The Boltzmann Distribution and Gases - UCalgary Chemistry Textbook

In the definition of kinetic molecular theory, we defined gases as a collection of particles in motion:

Statement 1: Gases are composed of particles that are in continuous motion, travelling in straight lines and changing direction only when they collide with other particles or with the walls of a container.

In a sample of a gas, the individual particles will be travelling at a variety of speeds and they are constantly colliding, transferring energy, and changing direction. However, because there are so many particles, the average speed is constant, as is the distribution of speeds (at least for a closed sample of gas at a constant temperature.

The distribution of molecular speeds for a sample of oxygen (O₂) at 300 K is shown in the figure below:

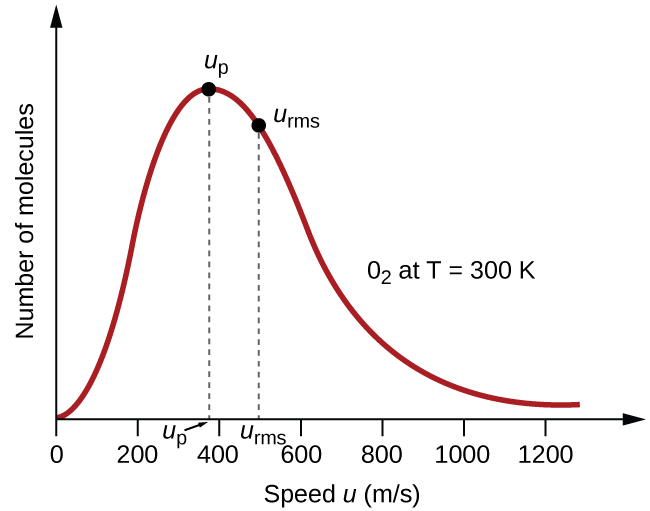
A graph is shown. The horizontal axis is labeled, “Speed u ( m divided by s ).” This axis is marked by increments of 20 beginning at 0 and extending up to 120. The vertical axis is labeled, “Fraction of molecules.” A positively or right-skewed curve is shown in red which begins at the origin and approaches the horizontal axis around 120 m per s. At the peak of the curve, a point is indicated with a black dot and is labeled, “v subscript p.” A vertical dashed line extends from this point to the horizontal axis at which point the intersection is labeled, “v subscript p.” Slightly to the right of the peak a second black dot is placed on the curve. This point is labeled, “v subscript r m s.” A vertical dashed line extends from this point to the horizontal axis at which point the intersection is labeled, “v subscript r m s.” The label, “O subscript 2 at T equals 300 K” appears in the open space to the right of the curve. — The molecular speed distribution for oxygen gas at 300 K is shown here. The most probable speed, u_p, is a little less than 400 m/s, while the root mean square speed, u_rms, is closer to 500 m/s.

Notice that in this distribution, very few molecules move at either very low or very high speeds. The number of molecules with intermediate speeds increases rapidly up to a maximum, which is the most probable speed, then drops off rapidly. Because of the long “tail” of faster-moving molecules, the average speed is slightly higher than the most probable speed.

This distribution of speeds is called the Boltzmann-Maxwell Distribution, after the two scientists who derived and refined it. This distribution is calculated using the formula
$$F(u) = 4\pi \left(\frac{M}{2\pi RT}\right)^{3/2}u^2 e^{-Mu^2 / 2RT}$$

where:
$F(u)$ is the fraction of gas particles having speed “$u$” (in m/s)
$M$ is the molar mass of the gas
$R$ is the ideal gas constant in Kelvin
$T$ is the Kelvin temperature of the gas.

From here, we can see that temperature and molar mass will affect the speed distribution of particles in our gas sample. In the next few pages, we’ll investigate the origins and implications of this for our observable gas properties.