6.6 Non-Ideal Gas Behaviour

Thus far, the ideal gas law, PV = nRT, has been applied to a variety of different types of problems, ranging from reaction stoichiometry and empirical and molecular formula problems to determining the density and molar mass of a gas. However the behavior of a real gas is often non-ideal, meaning that the observed relationships between its pressure, volume, and temperature are not accurately described by the ideal gas law.

Conditions for non-ideality

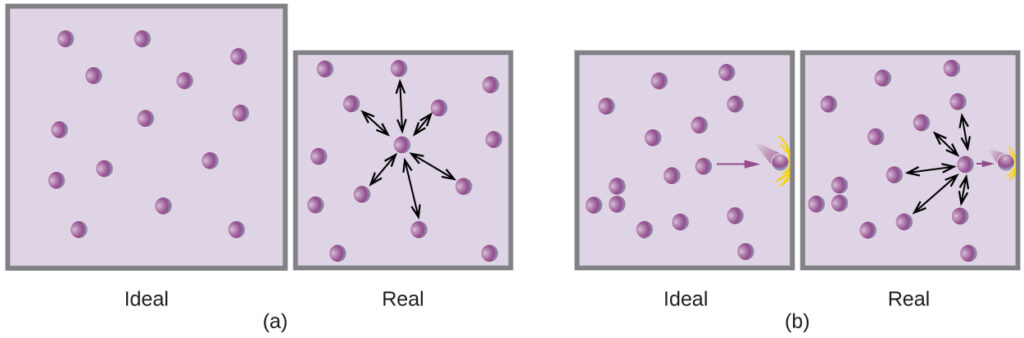
In defining our ideal gas (and kinetic molecular theory) previously, we made some assumptions about how gases behave, particularly:

  • Gas particles exert no attractive or repulsive forces on each other or the container walls.
  • The gas particles are negligibly small compared to the distances between them.

If either of these assumptions becomes untrue, then the approximation of ideal behaviour will fail to describe our gas. This primarily happens under two conditions:

Gases at high pressure

At high pressures, the particles of the gas have less room to move (more particles per unit volume), so they exist closer to each other. This can break both of the assumptions above:

  • The particles are closer together, so a relatively weak attractive or repulsive force will have more effect (where previously particles may have been too far apart to interact)
  • The volume of the actual gas particle (molecule or atom) may now be significant. With more particles in the same space, there is less empty space between the particles, so the space taken up by the particles themselves is a greater fraction of the total volume.

Gases at low temperature

At low temperatures, the particles of gas move more slowly, so they have more chance to interact with each other. If pressure is constant, the colder gas will also be more dense (particles are closer together, in a smaller volume) than for the same pressure at a higher temperature.

  • The particles move more slowly, so they exist near each other for a longer time. This gives the particles more chance to interact with each other, even if the forces are relatively weak).
  • If the gas is also more dense, then the particles are also closer together, with the same effect as the high pressure described above.

Effects of non-ideal behaviour

If a gas is not behaving “ideally”, the most common observation is that the gas will have a slightly lower volume and pressure than expected (by the ideal gas law). This is because attractive forces between the gas particles pulls them slightly more close together, reducing the overall volume, and reducing the force with which the particles are hitting the container walls:

This figure includes two diagrams. Each involves two lavender shaded boxes that contain 14 relatively evenly distributed, purple spheres. The first box in a on the left is labeled “ideal.” In the second slightly smaller box, on the right, a nearly centrally located purple sphere has 6 double-headed arrows extending outward from it to nearby spheres. This box is labeled “real.” In b, in the first box on the left, a single arrow points to a purple sphere at the right side that appears to be moving and impacting the right side of the box. There are no other spheres positioned near the right edge. This box is labeled “ideal.” The second box, on the right, shows the same image but has 5 double-headed arrows radiating out to the top, bottom, and left to other spheres. This box is labeled “real.”
(a) Attractions between gas molecules serve to decrease the gas volume at constant pressure compared to an ideal gas whose molecules experience no attractive forces. (b) These attractive forces will decrease the force of collisions between the molecules and container walls, therefore reducing the pressure exerted at constant volume compared to an ideal gas.

At very high pressure, the particle volume becomes most important, and the gas becomes harder to compress (taking up a larger than ideal volume). This is because the particles themselves cannot be compressed – when there is less space between them, it becomes more difficult to push the particles together.