Integration of the rate law for a simple first-order reaction $(rate=k[A])$ results in an equation describing how the reactant concentration varies with time: $$ ln(\frac{[A]_0}{ [A]_t })=kt \label{eq1}\tag{1}$$
where k is the rate constant, the initial concentration is [A]0 and [A]t is the concentration present after any given time t. This equation can be arranged to other formats for convenience:
$$ ln(\frac{[A]_t}{ [A]_0 })=-kt \label{eq2}\tag{2}$$
and a linearized version: $$ln[A]_t = -kt+ln[A]_0 \label{eq3}\tag{3}$$
Example: The Integrated Rate Law for a First-Order Reaction
The rate constant for the first-order decomposition of cyclobutane, C4H8 at 500 °C is 9.2 × 10−3 s−1: $$ C_4 H_8 \rightarrow 2\; C_2 H_ 4 $$
How long will it take for 80.0% of a sample of C4H8 to decompose?
Solution We use the integrated form of the rate law to answer questions regarding time: $ ln(\frac{[A]_0}{ [A]_t})=kt $
There are four variables in the rate law, so if we know three of them, we can determine the fourth. In this case we know [A]0, [A], and k, and need to find t.
The initial concentration of C4H8, [A]0, is not provided, but the provision that 80.0% of the sample has decomposed is enough information to solve this problem. Let x be the initial concentration, in which case the concentration after 80.0% decomposition is 20.0% of x or 0.200x. Rearranging the rate law to isolate t and substituting the provided quantities yields: $$ t=ln\frac {[x]}{[0.200x]}\times \frac{1}{k}\\
=ln(5)\times \frac{1}{9.2\times 10^{-3} s^{-1}} \\
=1.609 \times \frac{1}{9.2\times 10^{-3} s^{-1}} \\
=1.7\times 10^2 s $$
Check Your Learning
Iodine-131 is a radioactive isotope that is used to diagnose and treat some forms of thyroid cancer. Iodine-131 decays to xenon-131 according to the equation:
$$^{131}I \rightarrow \: ^{131}Xe\;+ \text{electron} $$The decay is first-order with a rate constant of 0.138 d−1. Knowing that all radioactive decay is first order, how many days will it take for exactly 90% of the iodine−131 in a 0.500 M solution of this substance to decay to Xe-131?
Answer:
If 90% of the I-131 has decaued, then 10% is left. In other words, if we started with 100 M of I-131, after the end of this time period, we will have 10 M.
Using the first-order integrated rate law (equation $\ref{eq1}$ above), we can see that the units in the ratio $ \frac{[A]_0}{ [A]_t} $ will cancel – so what units of concentration we input don’t matter, as long as that ratio (100:10) is maintained. We do not need to know the actual starting concentration: we can assume 100 if we want:
$$ ln \left(\frac{[A]_0}{ [A]_t } \right)=kt \\
ln \left(\frac{100 \, M}{10 \, M} \right)=(0.138 \text{d}^{-1})\, t \\
t = 16.6_{854} \text{d} \\
t = 16.7\: \text{days}$$
Note – since “90%” is a ratio, not a measured value, and is specified as “exact”, we can assume it to mean 90.0000000000… and it (and the numbers we derived from it – 100 and 10 M) will not affect the significant digits in the final answer.
We can use integrated rate laws with experimental data that consist of time and concentration information to determine the order and rate constant of a reaction. The integrated rate law can be rearranged to a standard linear equation format: $$ln[A]_t =−kt+ln[A]_0 \label{eq4}\tag{4} \\ y=mx+b$$
A plot of ln[A] versus t for a first-order reaction is a straight line with a slope of −k and an intercept of ln[A]0. If a set of rate data are plotted in this fashion but do not result in a straight line, the reaction is not first order in A.
Determination of Reaction Order by Graphing
Show that the data in the table below can be represented by a first-order rate law by graphing ln[H2O2] versus time. Determine the rate constant for the rate of decomposition of H2O2 from this data.
| Trial | Time (h) | [H2O2] (M) | ln[H2O2] |
|---|---|---|---|
| 1 | 0 | 1.000 | 0.0 |
| 2 | 6.00 | 0.500 | −0.693 |
| 3 | 12.00 | 0.250 | −1.386 |
| 4 | 18.00 | 0.125 | −2.079 |
| 5 | 24.00 | 0.0625 | −2.772 |
Solution: The data from the table above are plotted here:
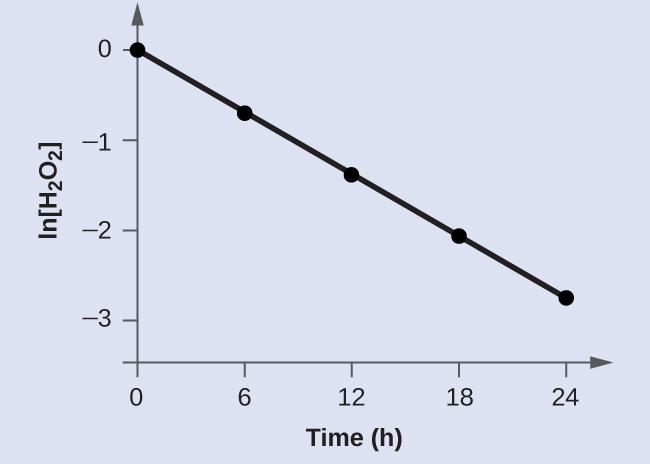
The plot of ln[H2O2] versus time is linear, thus we have verified that the reaction may be described by a first-order rate law.
The rate constant for a first-order reaction is equal to the negative of the slope of the plot of ln[H2O2] versus time where: $$ slope=\frac{change\;in\;y}{change\;in\;x}=\frac{\Delta y}{\Delta x}=\frac{\Delta ln[H_2 O_2]}{\Delta t} $$
In order to determine the slope of the line, we need two values of ln[H2O2] at different values of t (one near each end of the line is preferable). For example, the value of ln[H2O2] when t is 6.00 h is −0.693; the value when t = 12.00 h is −1.386: $$ \text{slope} =\frac{−1.386−(−0.693)}{12.00\;h−6.00\;h} \\ =\frac{−0.693}{6.00\;h} \\ =−1.155\times 10^{−1}\; h^{−1} \\ k=\, − \text{slope} =−(−1.155×10^{−1}h^{−1})=1.155\times 10^{−1}\, h^{−1} $$
Check Your Learning
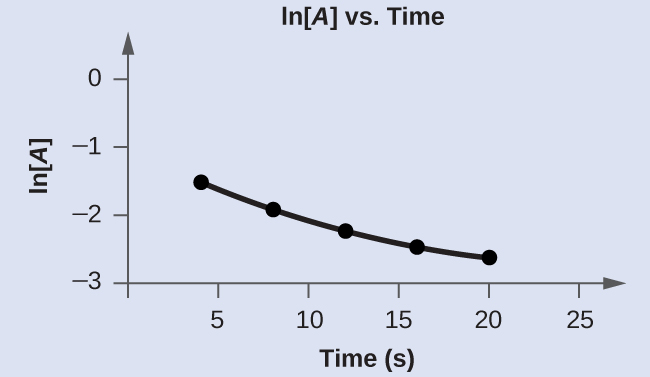
Graph the following data to determine whether the reaction $ A \rightarrow B+C$ is first order.
| Trial | Time (s) | [A] |
|---|---|---|
| 1 | 4.0 | 0.220 |
| 2 | 8.0 | 0.144 |
| 3 | 12.0 | 0.110 |
| 4 | 16.0 | 0.088 |
| 5 | 20.0 | 0.074 |
Answer:
The plot of ln[A] vs t is not a straight line. Therefore this reaction is not a first-order reaction.