$K_f$, or the formation constant for a complex, is one of the common “named equilibria” you will encounter (along with $K_a, K_b, K_w,$ and $K_{sp}$. A formation reaction will always have the form: $$ \text{ion} + \text{ligand} \rightleftharpoons \text{complex}$$.
As an example of dissolution by complex ion formation, let us consider what happens when we add aqueous ammonia to a mixture of silver chloride and water. Silver chloride dissolves slightly in water, giving a small concentration of Ag+ ([Ag+] = $1.3×10^{-5}\;M$):
$$AgCl\;(s)⇌Ag^+\;(aq)+Cl^-\;(aq)$$However, if NH3 is present in the water, the complex ion, $Ag(NH_3)_2^+$, can form according to the equation:
$$Ag^++2NH_3⇌Ag(NH_3)_2^+$$Dissociation of a Complex Ion
Calculate the concentration of the silver ion in a solution that initially is 0.10 M with respect to $Ag(NH_3)_2^+$
Solution
Applying the standard ICE approach to this reaction yields the following:
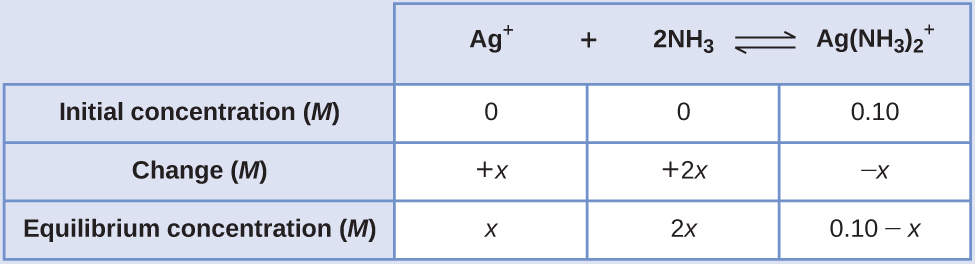
Substituting these equilibrium concentration terms into the Kf expression gives
$$K_f=\frac{[Ag(NH_3)_2^+]}{[Ag^+][NH_3]^2}$$ $$1.7×10^7=\frac{0.10-x}{(x)(2x)^2}$$The very large equilibrium constant means the amount of the complex ion that will dissociate, x, will be very small. Assuming x << 0.1 permits simplifying the above equation:
$$1.7×10^7=\frac{0.10}{(x)(2x)^2}$$ $$x^3=\frac{0.10}{4(1.7×10^7)}=1.5×10^{-9}$$ $$x=\sqrt[3]{1.5×10^{-9}}=1.1×10^{-3}$$Because only 1.1% of the $Ag(NH_3)_2^+$ dissociates into Ag+ and NH3, the assumption that x is small is justified.
Using this value of x and the relations in the above ICE table allows calculation of all species’ equilibrium concentrations:
$$[Ag^+]=0+x=1.1×10^{-3}\;M$$ $$[Ag^+]=0+2x=2.2×10^{-3}\;M$$ $$[Ag(NH_3)_2^+]=0.10-x=0.10-0.0011=0.099$$The concentration of free silver ion in the solution is 0.0011 M.
Calculate the silver ion concentration, [Ag+], of a solution prepared by dissolving 1.00 g of AgNO3 and 10.0 g of KCN in sufficient water to make 1.00 L of solution. (Hint: Because Kf is very large, assume the reaction goes to completion then calculate the [Ag+] produced by dissociation of the complex.)
Answer:
$2.9×10^{-22}\;M$