Brønsted-Lowry acid-base chemistry is the transfer of protons; thus, logic suggests a relation between the relative strengths of conjugate acid-base pairs. The strength of an acid or base is quantified in its ionization constant, Ka or Kb, which represents the extent of the acid or base ionization reaction. For the conjugate acid-base pair HA / A−, ionization equilibrium equations and ionization constant expressions are $$HA(aq)+H_2O(l)⇌H_3O^+(aq)+A^-(aq)\qquad K_a=\frac{[H_3O^+][A^-]}{[HA]}$$ $$A^-(aq)+H_2O(l)⇌OH^-(aq)+HA(aq)\qquad K_b=\frac{[HA][OH^-]}{[A^-]}$$
Adding these two chemical equations yields the equation for the autoionization for water: $$\require{enclose}\enclose{horizontalstrike}{HA(aq)}+H_2O(l)+\enclose{horizontalstrike}{A^-(aq)}+H_2O(l)⇌H_3O^+(aq)+\enclose{horizontalstrike}{A^-(aq)}+OH^-(aq)+\enclose{horizontalstrike}{HA(aq)}$$ $$2H_2O(l)⇌H_3O^+(aq)+OH^-(aq)$$
As discussed in another chapter on equilibrium, the equilibrium constant for a summed reaction is equal to the mathematical product of the equilibrium constants for the added reactions, and so $$K_a\times K_b=\frac{[H_3O^+][A^-]}{[HA]}\times \frac{[HA][OH^-]}{[A^-]}=[H_3O^+][OH^-]=K_w$$
This equation states the relation between ionization constants for any conjugate acid-base pair, namely, their mathematical product is equal to the ion product of water, Kw. By rearranging this equation, a reciprocal relation between the strengths of a conjugate acid-base pair becomes evident: $$K_a=\frac{K_w}{K_b}\;\text{or } K_b=\frac{K_w}{K_a}$$
The inverse proportional relation between Ka and Kb means the stronger the acid or base, the weaker its conjugate partner. The figure below illustrates this relation for several conjugate acid-base pairs.
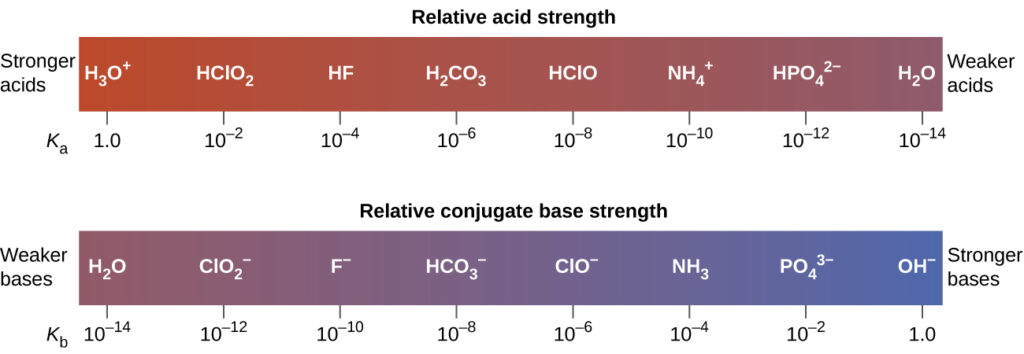
Relative strengths of several conjugate acid-base pairs are shown.
The listing of conjugate acid–base pairs in the table below is arranged to show the relative strength of each species as compared with water, whose entries are highlighted in each of the table’s columns.
In the acid column, those species listed below water are weaker acids than water. These species do not undergo acid ionization in water; they are not Bronsted-Lowry acids. All the species listed above water are stronger acids, transferring protons to water to some extent when dissolved in an aqueous solution to generate hydronium ions.
Species above water but below hydronium ion are weak acids, undergoing partial acid ionization, whereas those above hydronium ion are strong acids that are completely ionized in aqueous solution.
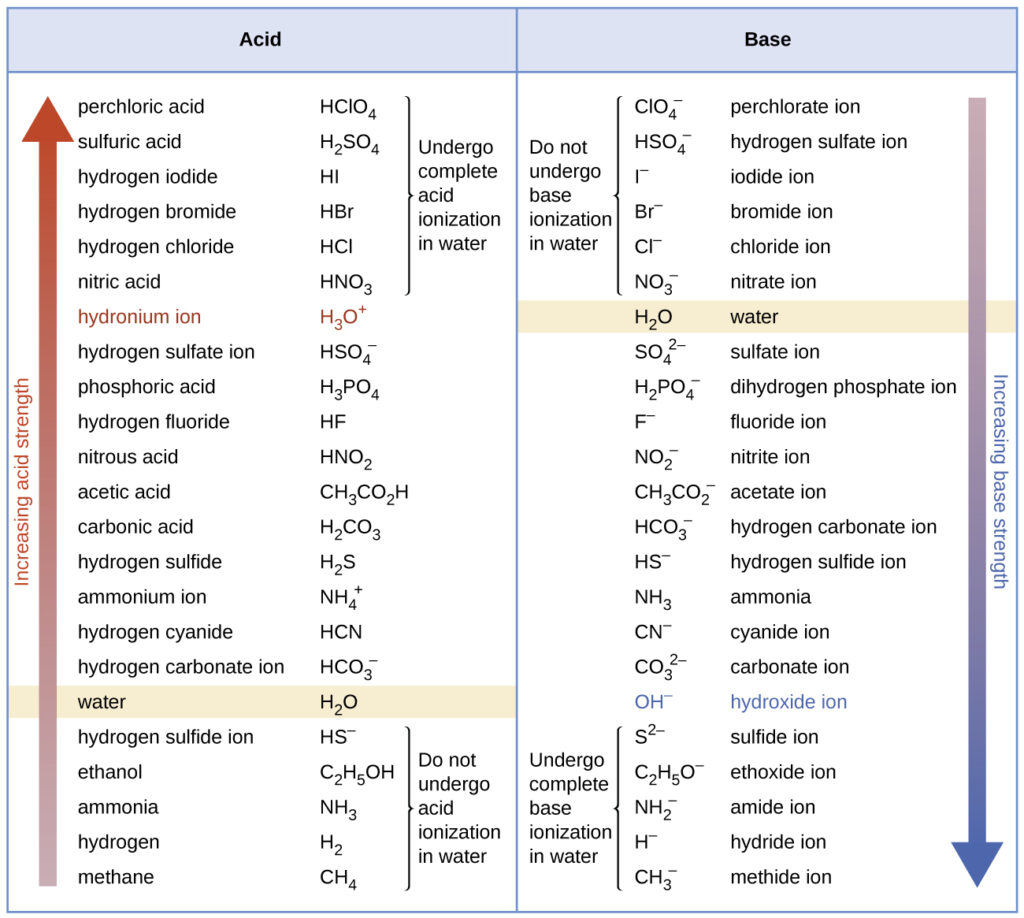
This figure shows strengths of conjugate acid-base pairs relative to the strength of water as the reference substance.
If all these strong acids are completely ionized in water, why does the column indicate they vary in strength, with nitric acid being the weakest and perchloric acid the strongest?
Notice that the sole acid species present in an aqueous solution of any strong acid is H3O+(aq), meaning that hydronium ion is the strongest acid that may exist in water; any stronger acid will react completely with water to generate hydronium ions. This limit on the acid strength of solutes in a solution is called a leveling effect. To measure the differences in acid strength for “strong” acids, the acids must be dissolved in a solvent that is less basic than water. In such solvents, the acids will be “weak,” and so any differences in the extent of their ionization can be determined. For example, the binary hydrogen halides HCl, HBr, and HI are strong acids in water but weak acids in ethanol (strength increasing HCl < HBr < HI).
The right column of the table above lists a number of substances in order of increasing base strength from top to bottom. Following the same logic as for the left column, species listed above water are weaker bases and so they don’t undergo base ionization when dissolved in water. Species listed between water and its conjugate base, hydroxide ion, are weak bases that partially ionize. Species listed below hydroxide ion are strong bases that completely ionize in water to yield hydroxide ions (i.e., they are leveled to hydroxide). A comparison of the acid and base columns in this table supports the reciprocal relation between the strengths of conjugate acid-base pairs. For example, the conjugate bases of the strong acids (top of table) are all of negligible strength. A strong acid exhibits an immeasurably large Ka, and so its conjugate base will exhibit a Kb that is essentially zero:
Strong acid: $K_a ≈ ∞$
conjugate base: $K_b=K_w/K_a=K_w/∞≈0$
A similar approach can be used to support the observation that conjugate acids of strong bases (Kb ≈ ∞) are of negligible strength (Ka ≈ 0).
Calculating Ionization Constants for Conjugate Acid-Base Pairs
Use the Kb for the nitrite ion, $NO_2^-$, to calculate the Ka for its conjugate acid.
SolutionKb for $NO_2^-$ is given in this section as $2.17×10^{-11}$. The conjugate acid of $NO_2^-$ is HNO2; Ka for HNO2 can be calculated using the relationship:
$$K_a\times K_b=1.0×10^{-14}=K_w$$Solving for Ka yields
$$K_a=\frac{K_w}{K_b}=\frac{1.0×10^{-14}}{2.17×10^{-11}}=4.6×10^{-4}$$This answer can be verified by finding the Ka for HNO2 in here.
Check Your Learning
Determine the relative acid strengths of $NH_4^+$ and HCN by comparing their ionization constants. The ionization constant of HCN is given here as $4.9×10^{-10}$. The ionization constant of $NH_4^+$ is not listed, but the ionization constant of its conjugate base, NH3, is listed as $1.8×10^{-5}$.
Answer:
$NH_4^+$ is the slightly stronger acid (Ka for $NH_4^+= 5.6×10^{-10}$).