Another useful thing we can do about titrations is to predict the pH and solution composition at various points in the titration. This lets us (for example) stop the titration at a target pH or composition, rather than the endpoint, or test whether the experiment design we are trying to use will produce a clear endpoint on a pH titration curve.
When doing titration calculations, there are 4 main “regions” of the titration, that correspond to calculation strategies:
- Initial conditions – the system as it was built; no titrant has been added yet
- Buffer region – we have a mix of the conjugate acid and base in solution now (the half-equivalence point is the center of this region)
- Equivalence point – The analyte has been perfectly neutralized; the only thing in solution is its conjugate
- After equivalence – pH is determined by the excess titrant that we have added.
Our titrant will always be a strong acid or base (in this course).
For titrations where the analyte is a strong base or acid as well, all the calculations are simple stoichiometry and pH is determined by whichever ($H^+$ or $OH^-$) is in excess. Titrations where the analyte is a weak base or acid will need equilibrium / ICE table calculations in all regions except “after equivalence” (where the pH is set by excess titrant, which is a strong acid or base).
The following examples work through these kinds of titration calculations:
Calculating pH for Titration Solutions: Strong Acid/Strong Base
A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH (the titration curve is shown in [link]). Calculate the pH at these volumes of added base solution:
(a) 0.00 mL
(b) 12.50 mL
(c) 25.00 mL
(d) 37.50 mL
Solution
(a) Titrant volume = 0 mL. The solution pH is due to the acid ionization of HCl. Because this is a strong acid, the ionization is complete and the hydronium ion molarity is 0.100 M. The pH of the solution is then
(b) Titrant volume = 12.50 mL. Since the acid sample and the base titrant are both monoprotic and equally concentrated, this titrant addition involves less than a stoichiometric amount of base, and so it is completely consumed by reaction with the excess acid in the sample. The concentration of acid remaining is computed by subtracting the consumed amount from the initial amount and then dividing by the solution volume:
$$[H_3O^+]=\frac{n(H^+)}{V}=\frac{0.002500\;mol\times\left(\frac{1000\;mL}{1\;L}\right)-0.100\;M\times12.50\;mL}{25.00\;mL+12.50\;mL}=0.0333\;M$$(c) Titrant volume = 25.00 mL. This titrant addition involves a stoichiometric amount of base (the equivalence point), and so only products of the neutralization reaction are in solution (water and NaCl). Neither the cation nor the anion of this salt undergo acid-base ionization; the only process generating hydronium ions is the autoprotolysis of water. The solution is neutral, having a pH = 7.00.
(d) Titrant volume = 37.50 mL. This involves the addition of titrant in excess of the equivalence point. The solution pH is then calculated using the concentration of hydroxide ion:
$$n(OH^-)_0>n(H^+)_0$$ $$[OH^-]=\frac{n(OH^-)}{V}=\frac{0.100\;M\times 37.50\;mL-0.002500\;mol\times\left(\frac{1000\;mL}{1\;L}\right)}{25.00\;mL+37.50\;mL}=0.0200\;M$$pH = 14 − pOH = 14 + log([OH−]) = 14 + log(0.0200) = 12.30
Check Your Learning
Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO3(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.
Answer:
0.00: 1.000; 15.0: 1.5111; 25.0: 7; 40.0: 12.523
Titration of a Weak Acid with a Strong Base
Consider the titration of 25.00 mL of 0.100 M CH3CO2H with 0.100 M NaOH. The reaction can be represented as:
Calculate the pH of the titration solution after the addition of the following volumes of NaOH titrant:
(a) 0.00 mL
(b) 25.00 mL
(c) 12.50 mL
(d) 37.50 mL
Solution
(a) The initial pH is computed for the acetic acid solution in the usual ICE approach:
(b) The acid and titrant are both monoprotic and the sample and titrant solutions are equally concentrated; thus, this volume of titrant represents the equivalence point. Unlike the strong-acid example above, however, the reaction mixture in this case contains a weak conjugate base (acetate ion). The solution pH is computed considering the base ionization of acetate, which is present at a concentration of
$$\frac{0.00250\;mol}{0.0500\;L}=0.0500\;M\;CH_3CO_2^-$$Base ionization of acetate is represented by the equation
$$CH_3CO_2^-\;(aq)+H_2O\;(l)⇌CH_3CO_2H\;(aq)+OH^-\;(aq)$$ $$K_b=\frac{[H^+][OH^-]}{K_a}=\frac{K_w}{K_a}=\frac{1.0×10^{-14}}{1.8×10^{-5}}=5.6×10^{-10}$$Assuming x << 0.0500, the pH may be calculated via the usual ICE approach:
$$K_b=\frac{x^2}{0.0500\;M}$$ $$x=[OH^-]=5.3×10^{-6}$$ $$\text{pOH}=-log(5.3×10^{-6})=5.28$$ $$\text{pH}=14.00-5.28=8.72$$Note that the pH at the equivalence point of this titration is significantly greater than 7, as expected when titrating a weak acid with a strong base.
(c) Titrant volume = 12.50 mL. This volume represents one-half of the stoichiometric amount of titrant, and so one-half of the acetic acid has been neutralized to yield an equivalent amount of acetate ion. The concentrations of these conjugate acid-base partners, therefore, are equal. A convenient approach to computing the pH is use of the Henderson-Hasselbalch equation:
$$\text{pH}=pK_a+log\frac{[\text{Base}]}{[\text{Acid}]}=-log(K_a)+log\frac{[CH_3CO_2^-]}{[CH_3CO_2H]}=-log(1.8×10^{-5})+log(1)$$ $$\text{pH}=-log(1.8×10^{-5})=4.74$$(pH = pKa at the half-equivalence point in a titration of a weak acid)
(d) Titrant volume = 37.50 mL. This volume represents a stoichiometric excess of titrant, and a reaction solution containing both the titration product, acetate ion, and the excess strong titrant. In such solutions, the solution pH is determined primarily by the amount of excess strong base:
$$[OH^-]=\frac{(0.003750\;mol-0.00250\;mol)}{0.06250\;L}=2.00×10^{-2}\;M$$ $$\text{pOH}=-log(2.00×10^{-2})=1.70\text{, and pH}=14.00-1.70=12.30$$Check Your Learning
Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.
Answer:
0.00 mL: 2.37; 15.0 mL: 3.92; 25.00 mL: 8.29; 30.0 mL: 12.097
A summary of pH/volume data pairs for the strong and weak acid titrations is provided in the table below and plotted as titration curves following. Analyzing this more complete data highlights some interesting differences between the “weak” and “strong” analyte in each titration region:
- Initial conditions: The initial pH is determined by the acid being titrated. Because the two acid samples are equally concentrated, the weak acid will exhibit a greater initial pH.
- Buffer region: We see the pH changing gradually (the “strong acid” system does not technically have a buffer, but since pH is a log scale, the change in concentration of the acid is slow). Notice the difference in shape of the two curves in this region as well.
- Equivalence point: the pH of the strong-acid system is 7.00 (perfectly neutral) since there is only water and non-pH-active ions at this point. The weak-acid system contains the conjugate base (a true weak base) at this point, so its pH is just above 7. (Consider: what pH would you expect if you were titrating a weak-base analyte?)
- After equivalence: Both acids had the same concentration and titrant, so since this region is determined only by the excess titrant, they are similar.
| pH Values in the Titrations of a Strong Acid and of a Weak Acid | |||
|---|---|---|---|
| Volume of 0.100 M NaOH Added (mL) | Moles of NaOH Added | pH Values 0.100 M HCl1 | pH Values 0.100 M CH3CO2H2 |
| 0.0 | 0.0 | 1.00 | 2.87 |
| 5.0 | 0.00050 | 1.18 | 4.14 |
| 10.0 | 0.00100 | 1.37 | 4.57 |
| 15.0 | 0.00150 | 1.60 | 4.92 |
| 20.0 | 0.00200 | 1.95 | 5.35 |
| 22.0 | 0.00220 | 2.20 | 5.61 |
| 24.0 | 0.00240 | 2.69 | 6.13 |
| 24.5 | 0.00245 | 3.00 | 6.44 |
| 24.9 | 0.00249 | 3.70 | 7.14 |
| 25.0 | 0.00250 | 7.00 | 8.72 |
| 25.1 | 0.00251 | 10.30 | 10.30 |
| 25.5 | 0.00255 | 11.00 | 11.00 |
| 26.0 | 0.00260 | 11.29 | 11.29 |
| 28.0 | 0.00280 | 11.75 | 11.75 |
| 30.0 | 0.00300 | 11.96 | 11.96 |
| 35.0 | 0.00350 | 12.22 | 12.22 |
| 40.0 | 0.00400 | 12.36 | 12.36 |
| 45.0 | 0.00450 | 12.46 | 12.46 |
| 50.0 | 0.00500 | 12.52 | 12.52 |
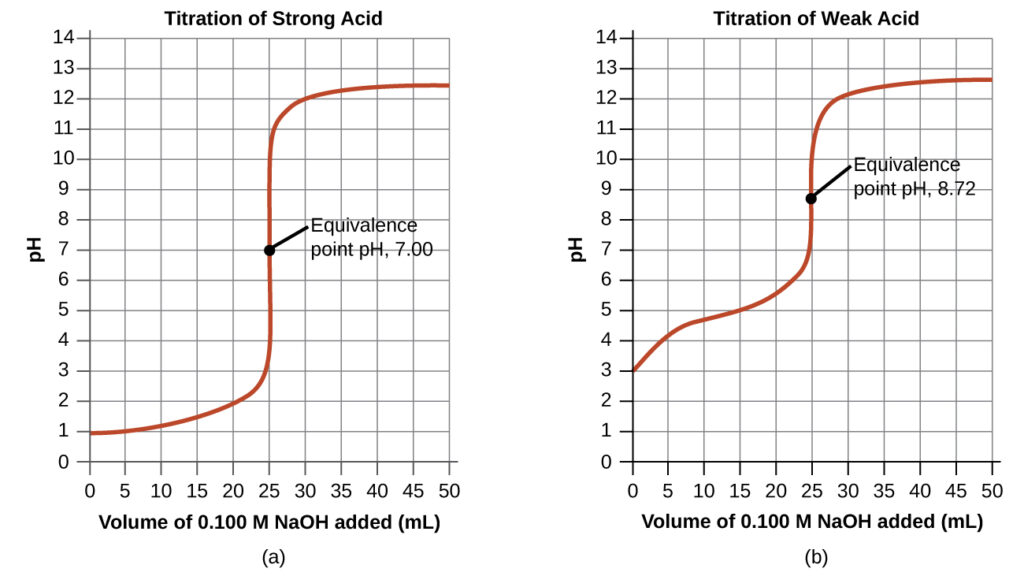
(a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M acetic acid (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.