Measuring pH directly requires an expensive pH probe, and either a computer to plot the pH data, or extensive hand-plotting. For titrations where we are only concerned about the equivalence point volume, a colour indicator is a simpler and easier way to detect the equivalence point.
pH colour indicators are molecules that:
a) are a weak acid or base (so they react with hydronium)
b) have conjugate acid and base forms that are differently coloured.
In an acidic solution, the colour indicator will exist in its conjugate acid form (one colour), but as base is added and pH increases, it is converted to its conjugate base form (another colour). We will notice the change in colour near the pKa of the indicator (explanation below).
When writing a reaction involving an indicator, we often use the abbreviations $\mathbf{HIn}$ for the acid form of the indicator and $\mathbf{In^-}$ for the base form, since many indicators have complex chemical structures (and chemists can be lazy!).
The equilibrium in a solution of the acid-base colour indicator methyl orange can be represented like this:
$$ \frac{HIn\;(aq) + H_2O\;(l)\rightleftharpoons H_3O^+\;(aq) + In^-\;(aq)}{\text{RED}\qquad \qquad \qquad \qquad \qquad \qquad \quad \text{YELLOW}} \qquad \qquad K_a=\frac{[H_3O^+][In^-]}{[HIn]}=4.0×10^{-4}$$
The anion of methyl orange, In−, is yellow, and the protonated form, HIn, is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form.
The perceived color of an indicator solution is determined by the ratio of the concentrations of the two species In− and HIn. If most of the indicator (typically about 60−90% or more) is present as In−, we will see the color of the solution as yellow. If most is present as HIn, then the solution color appears red. The Henderson-Hasselbalch equation is useful for understanding the relationship between the pH of an indicator solution and its composition (thus, perceived color):
$$\text{pH}=\text{p}K_a+log\left(\frac{[In^-]}{[HIn]}\right)$$
In solutions where pH > pKa, the logarithmic term must be positive, indicating an excess of the conjugate base form of the indicator (yellow solution). When pH < pKa, the log term must be negative, indicating an excess of the conjugate acid (red solution). When the solution pH is close to the indicator pKa, appreciable amounts of both conjugate partners are present, and the solution color is that of an additive combination of each (yellow and red, yielding orange). The color change interval (or pH interval) for an acid-base indicator is defined as the range of pH values over which a change in color is observed, and for most indicators this range is approximately pKa ± 1.
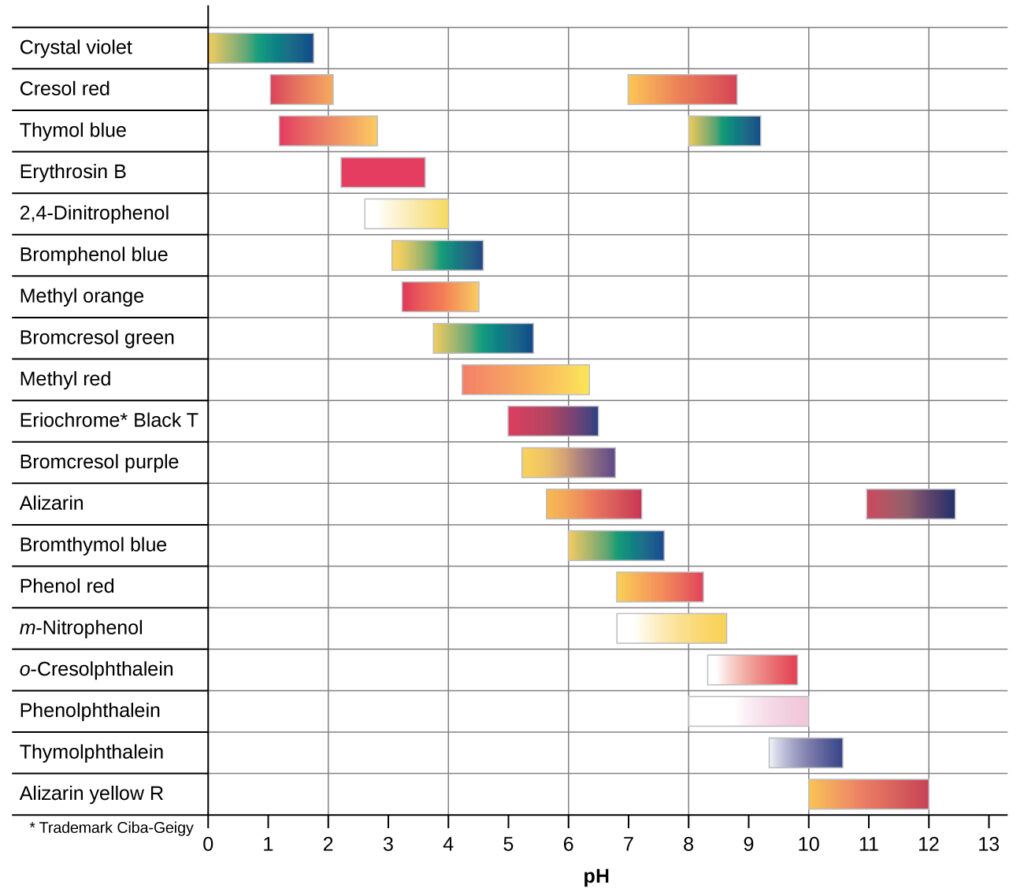
There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. The chart below presents several indicators, their colors, and their color-change intervals.
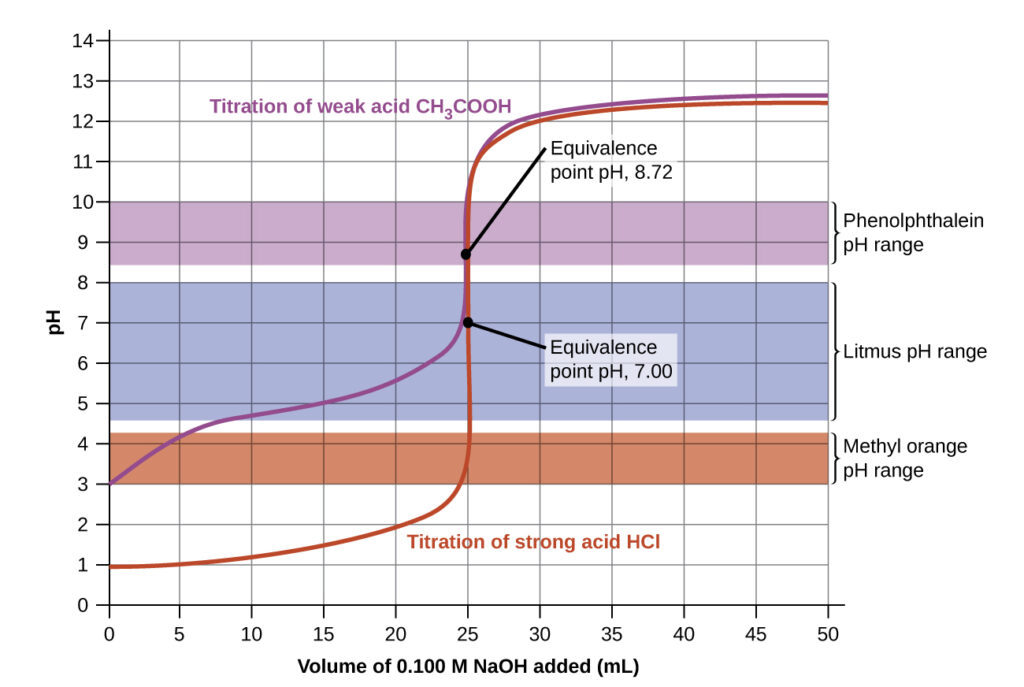
Titration curves for strong and weak acids illustrating the proper choice of acid-base indicator. Any of the three indicators will exhibit a reasonably sharp color change at the equivalence point of the strong acid titration, but only phenolphthalein is suitable for use in the weak acid titration.
The titration curves shown in the figure above illustrate the choice of a suitable indicator for specific titrations. In the strong acid titration, use of any of the three indicators should yield reasonably sharp color changes and accurate end point determinations. For this titration, the solution pH reaches the lower limit of the methyl orange color change interval after addition of ~24 mL of titrant, at which point the initially red solution would begin to appear orange. When 25 mL of titrant has been added (the equivalence point), the pH is well above the upper limit and the solution will appear yellow. The titration’s end point may then be estimated as the volume of titrant that yields a distinct orange-to-yellow color change. This color change would be challenging for most human eyes to precisely discern. More-accurate estimates of the titration end point are possible using either litmus or phenolphthalein, both of which exhibit color change intervals that are encompassed by the steep rise in pH that occurs around the 25.00 mL equivalence point.
The weak acid titration curve above shows that only one of the three indicators is suitable for end point detection. If methyl orange is used in this titration, the solution will undergo a gradual red-to-orange-to-yellow color change over a relatively large volume interval (0–6 mL), completing the color change well before the equivalence point (25 mL) has been reached. Use of litmus would show a color change that begins after adding 7–8 mL of titrant and ends just before the equivalence point. Phenolphthalein, on the other hand, exhibits a color change interval that nicely brackets the abrupt change in pH occurring at the titration’s equivalence point. A sharp color change from colorless to pink will be observed within a very small volume interval around the equivalence point.
| What is your confidence level on this material after reading this Acid/Base Equilibrium chapter? Choose either Green (confident), Yellow (somewhat confident), Red (not confident). |
|---|