The numerical value of the reaction quotient Q varies as a reaction proceeds towards equilibrium; therefore, it can serve as a useful indicator of the reaction’s status. To illustrate this point, consider the oxidation of sulfur dioxide:
$$2SO_2\mathit (g) + O_2\mathit (g) ⇌ 2SO_3\mathit (g)$$
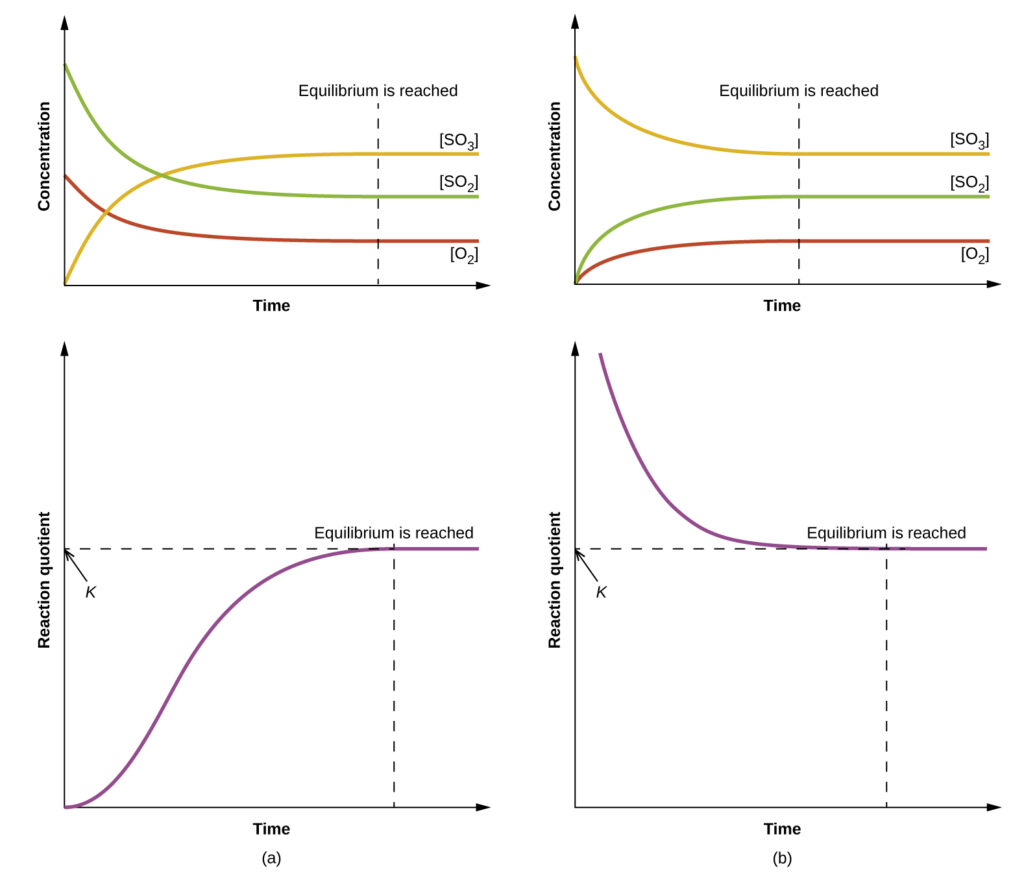
Two different experimental scenarios are depicted in the figure above, one in which this reaction is initiated with a mixture of reactants only, SO2 and O2, and another that begins with only product, SO3. For the reaction that begins with a mixture of reactants only, Q is initially equal to zero:
$$Q_c=\frac{[SO_3]^2}{[SO_2]^2[O_2]}=\frac{0^2}{[SO_2]^2[O_2]}=0$$
As the reaction proceeds toward equilibrium in the forward direction, reactant concentrations decrease (as does the denominator of Qc), product concentration increases (as does the numerator of Qc), and the reaction quotient consequently increases. When equilibrium is achieved, the concentrations of reactants and product remain constant, as does the value of Qc.
If the reaction begins with only product present, the value of Qc is initially undefined (immeasurably large, or infinite):
$$Q_c=\frac{[SO_3]^2}{[SO_2]^2[O_2]}=\frac{[SO_3]^2}{0}\:\qquad \: Q_c \rightarrow \infty$$
In this case, the reaction proceeds toward equilibrium in the reverse direction. The product concentration and the numerator of Qc decrease with time, the reactant concentrations and the denominator of Qc increase, and the reaction quotient consequently decreases until it becomes constant at equilibrium.
The constant value of Q exhibited by a system at equilibrium is called the equilibrium constant, K:
$$K≡Q\: \text{ at equilibrium}$$
Comparison of the data plots in Figure 1 shows that both experimental scenarios resulted in the same value for the equilibrium constant. This is a general observation for all equilibrium systems, known as the law of mass action: At a given temperature, the reaction quotient for a system at equilibrium is constant.
Evaluating a Reaction Quotient
Gaseous nitrogen dioxide forms dinitrogen tetroxide according to this equation:
When 0.10 mol NO2 is added to a 1.0-L flask at 25 °C, the concentration changes so that at equilibrium, [NO2] = 0.016 M and [N2O4] = 0.042 M.
(a) What is the value of the reaction quotient before any reaction occurs?
(b) What is the value of the equilibrium constant for the reaction?
SolutionAs for all equilibrium calculations in this text, use the simplified equations for Q and K and disregard any concentration or pressure units, as noted previously in this section.
(a) Before any product is formed, $$[NO_2]=\frac{0.10\, \text{mol}}{1.0 \, \text{L}}=0.10 \, \text{M}$,and $[N_2O_4]=0 \, \text{M}\\ Q_c=\frac{[N_2O_4]}{[NO_2]^2}\\ \mathbf{Q_c =\frac{0\, \text{M}}{[0.10\, \text{M}]^2}=0}$$. This reaction is not at equilibrium.
(b) At equilibrium,$K_c =Q_c =\frac{[N_2O_4]}{[NO_2]^2}=\frac{0.042\, \text{M}}{[0.016\, \text{M}]^2}=1.6×10^2$.
The equilibrium constant $\mathbf{K_c = 1.6×10^2}$.
Check Your Learning
For the reaction $$2SO_2\mathit (g) + O_2\mathit (g) \rightleftharpoons 2SO_3\mathit (g)$$ the concentrations at equilibrium are [SO2] = 0.90 M, [O2] = 0.35 M, and [SO3] = 1.1 M. What is the value of the equilibrium constant, Kc under these conditions?
Answer:
Start by writing the equilibrium expression for the reaction: $$ K_c = \frac{[SO_3]^2}{[SO_2]^2 [O_2]}$$ Substitute in the provided values: $$ K_c = \frac{[1.1\, \text{M}]^2}{[0.90\, \text{M}]^2 [0.35\, \text{M}]} \\ K_c = 4.2_{680776} \\ \mathbf{K_c = 4.3}$$