Relative Rates of Reaction

The rate of a reaction may be expressed as the change in concentration of any reactant or product. For any given reaction, these rate expressions are all related simply to one another according to the reaction stoichiometry. The rate of the general reaction $$aA\; \rightarrow\; bB$$ can be expressed in terms of rate of disappearance of A or the rate of appearance of B. These two rate expressions are related by the stoichiometry of the reaction: $$\text{rate of reaction}=-\left(\frac{1}{a}\right)\left(\frac{ΔA}{Δt}\right)=\left(\frac{1}{b}\right)\left(\frac{ΔB}{Δt}\right)$$

For example: if the reaction stoichiometry is: $$A\; \rightarrow\; 2B$$ then for each molecule of A that is consumed, two molecules of B are produced. Therefore we will expect the rate of appearance of B to be twice as large as the rate of disappearance of A (and since the rate of disappearance is negative, a negative sign is needed to make them equal. $$ -\left(\frac{1}{1}\right)\left(\frac{ΔA}{Δt}\right)=\left(\frac{1}{2}\right)\left(\frac{ΔB}{Δt}\right)$$

To prove to yourself this relation works, consider the scenario: if our reactant A was decreasing at 2 M/s, we know that B should be increasing at twice that, since each A produces two B’s. (so our rate of appearance of B must be 4 M/s.). That gives: $$ -\left(\frac{1}{1}\right)\left(\frac{-2\; M}{s}\right)=\left(\frac{1}{2}\right)\left(\frac{4\; M}{s}\right) \\ 2 = 2$$

Calculating Relative Rates

Consider the reaction represented by the following equation: $$2NH_3(g)⟶N_2(g)+3H_2(g)$$ If the general rate of reaction is $1.25\times 10^{-6} \frac{\text{mol/L}}{s}$, calculate the rates of appearance or disappearance of each reaction component.

Solution:

Taking the general formula for converting relative rates above and making it specific to this reaction, we have: $$\text{rate of reaction}\; = \; -\frac{1}{2}\frac{\Delta [NH_3]}{\Delta t} = \frac{1}{1}\frac{\Delta [N_2]}{\Delta t} = \frac{1}{3}\frac{\Delta [H_2]}{\Delta t}$$.

Solving for each reactant and product:

Ammonia (NH3)

$$\text{rate of reaction}\; = \; -\frac{1}{2}\frac{\Delta [NH_3]}{\Delta t} \\ 1.25\times 10^{-6} \frac{\text{mol/L}}{s}\; =\; -\frac{1}{2}\frac{\Delta [NH_3]}{\Delta t} \\ -2.50 \times 10^{-6}\frac{\text{mol/L}}{s}\;=\; \frac{\Delta [NH_3]}{\Delta t}$$

Nitrogen (N2)

$$\text{rate of reaction}\; = \; \frac{1}{1}\frac{\Delta [N_2]}{\Delta t} \\ 1.25\times 10^{-6} \frac{\text{mol/L}}{s}\; =\; -\frac{1}{1}\frac{\Delta [N_2]}{\Delta t} \\ 1.25\times 10^{-6} \frac{\text{mol/L}}{s}\;=\; \frac{\Delta [N_2]}{\Delta t}$$

Hydrogen (H2)

$$\text{rate of reaction}\; = \; \frac{1}{3}\frac{\Delta [H_2]}{\Delta t} \\ 1.25\times 10^{-6} \frac{\text{mol/L}}{s}\; =\; -\frac{1}{3}\frac{\Delta [H_2]}{\Delta t} \\ 3.75\times 10^{-6} \frac{\text{mol/L}}{s}\;=\; \frac{\Delta [H_2]}{\Delta t}$$

The figure below illustrates the change in concentrations over time for the decomposition of ammonia into nitrogen and hydrogen at 1100 °C. Slopes of the tangent lines at t = 500 s show that the instantaneous rates derived from all three species involved in the reaction are related by their stoichiometric factors. The rate of hydrogen production, for example, is observed to be three times greater than that for nitrogen production:

$$\frac{2.91×10^{-6}\;M/s}{9.70×10^{-7}\;M/s}≈3$$


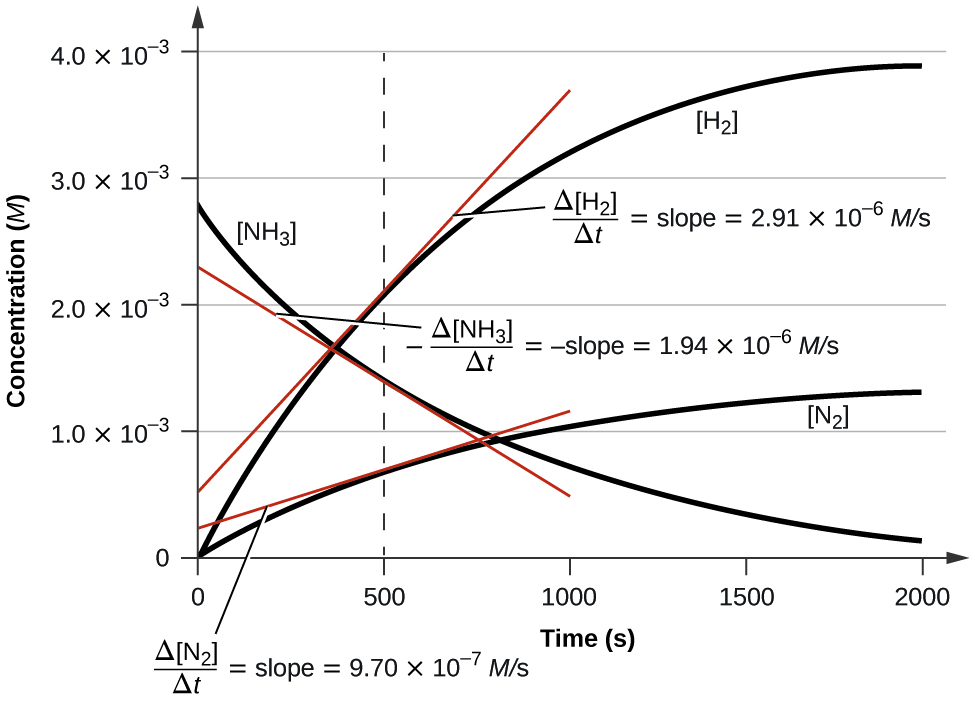
Changes in concentrations of the reactant and products for the reaction 2NH3 ⟶ N2 + 3H2.
The rates of change of the three concentrations are related by the reaction stoichiometry, as shown by the different slopes of the tangents at t = 500 s.

Expressions for Relative Reaction Rates
The first step in the production of nitric acid is the combustion of ammonia:

$$4NH_3(g)+5O_2(g)⟶4NO(g)+6H_2O(g)$$

Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.

Solution


Considering the stoichiometry of this homogeneous reaction, the rates for the consumption of reactants and formation of products are:

$$-\frac{1}{4}\frac{Δ[NH_3]}{Δt}=-\frac{1}{5}\frac{Δ[O_2]}{Δt}=\frac{1}{4}\frac{Δ[NO]}{Δt}=\frac{1}{6}\frac{Δ[H_2O]}{Δt}$$

Check Your Learning
The rate of formation of Br2 is $6.0×10^{-6}$ mol/L/s in a reaction described by the following net ionic equation:

$$5Br^-+BrO_3^-+6H^+⟶3Br_2+3H_2O$$

Reaction Rate Expressions for Decomposition of H2O2
The graph above shows the rate of decomposition of H2O2 over time:

$$2H_2O_2⟶2H_2O+O_2$$

Based on these data, the instantaneous rate of decomposition of H2O2 at t = 11.1 h is determined to be $3.20×10^{-2}$ mol/L/h, that is:

$$-\frac{Δ[H_2O_2]}{Δt}=3.20×1-^{-2}\;mol\;L^{-1}\;h^{-1}$$

What is the instantaneous rate of production of H2O and O2?

Solution

The reaction stoichiometry shows that

$$-\frac{1}{2}\frac{Δ[H_2O_2]}{Δt}=\frac{1}{2}\frac{Δ[H_2O]}{Δt}=\frac{Δ[O_2]}{Δt}$$

Therefore:

$$\frac{1}{2}\times 3.20×10^{-2}\;mol\;L^{-1}\;h^{-1}=\frac{Δ[O_2]}{Δt}$$

and

$$\frac{Δ[O_2]}{Δt}=1.60×10^{-2}\;mol\;L^{-1}\;h^{-1}$$

Check Your Learning
If the rate of decomposition of ammonia, NH3, at 1150 K is $2.10×10^{-6}$ mol/L/s, what is the rate of production of nitrogen and hydrogen?
Hint: Start by writing out the reaction. All compounds involved are named in the question.