How Buffers Work
To illustrate the function of a buffer solution, consider a mixture of roughly equal amounts of acetic acid and sodium acetate. The presence of a weak conjugate acid-base pair in the solution imparts the ability to neutralize modest amounts of added strong acid or base. For example, adding strong base to this solution will neutralize hydronium ion and shift the acetic acid ionization equilibrium to the right and generate additional ammounts of the weak conjugate base (acetate ion):
$$CH_3CO_2H\;(aq)+H_2O\;(l)⇌H_3O^+\;(aq)+CH_3CO_2^-\;(aq)$$Likewise, strong acid added to this buffer solution will shift the above ionization equilibrium left, producing additional amounts of the weak conjugate acid (acetic acid). [link] provides a graphical illustration of the changes in conjugate-partner concentration that occur in this buffer solution when strong acid and base are added. The buffering action of the solution is essentially a result of the added strong acid and base being converted to the weak acid and base that make up the buffer’s conjugate pair. The weaker acid and base undergo only slight ionization, as compared with the complete ionization of the strong acid and base, and the solution pH, therefore, changes much less drastically than it would in an unbuffered solution.
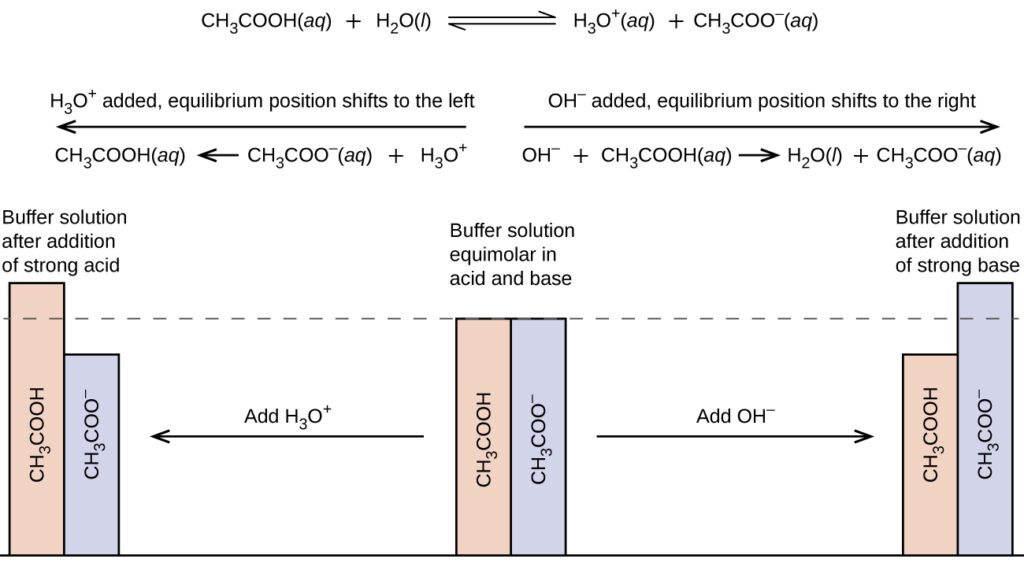
Buffering action in a mixture of acetic acid and acetate salt.
pH Changes in Buffered and Unbuffered Solutions
Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might affect the biochemical activity of these compounds.
(a) Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid and 0.10 M sodium acetate.
(b) Calculate the pH after 1.0 mL of 0.10 NaOH is added to 100 mL of this buffer.
(c) For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution with a pH of 4.74.
Solution
(a) Following the ICE approach to this equilibrium calculation yields the following:
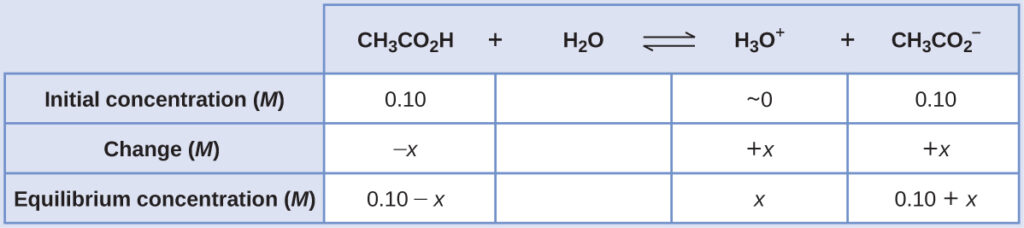
Substituting the equilibrium concentration terms into the $K_a$ expression, assuming x << 0.10, and solving the simplified equation for x yields
$$x=1.8×10^{-5}\;M$$ $$[H_3O^+]=0+x=1.8×10^{-5}\;M$$ $$\text{pH}=-log[H_3O^+]=-log(1.8×10^{-5})$$ $$=4.74$$(b) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer.
Adding strong acid will neutralize some of the acetic acid, yielding the conjugate base acetate ion. Compute the new concentrations of these two buffer components, then repeat the equilibrium calculation of part (a) using these new concentrations.
$$0.0010\;\require{enclose}\enclose{horizontalstrike}{L}x\left(\frac{0.10\;mol\;NaOH}{1\;\enclose{horizontalstrike}{L}}\right)=1.0×10^{-4}\;mol\;NaOH$$The initial molar amount of acetic acid is
$$0.100\;\enclose{horizontalstrike}{L}x\left(\frac{0.100\;mol\;CH_3CO_2H}{1\;\enclose{horizontalstrike}{L}}\right)=1.00×10^{-2}\;mol\;CH_3CO_2H$$The amount of acetic acid remaining after some is neutralized by the added base is
$$(1.0×10^{-2})-(0.01×10^{-2})=0.99×10^{-2}\;mol\;CH_3CO_2H$$The newly formed acetate ion, along with the initially present acetate, gives a final acetate concentration of
$$(1.0×10^{-2})+(0.01×10^{-2})=1.01×10^{-2}\;mol\;NaCH_3CO_2$$Compute molar concentrations for the two buffer components:
$$[CH_3CO_2H]=\frac{9.9×10^{-3}\;mol}{0.101\;L}=0.098\;M$$ $$[NaCH_3CO_2]=\frac{1.01×10^{-2}\;mol}{0.101\;L}=0.100\;M$$Using these concentrations, the pH of the solution may be computed as in part (a) above, yielding pH = 4.75 (only slightly different from that prior to adding the strong base).
(c) For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution with a pH of 4.74.
The amount of hydronium ion initially present in the solution is
$$[H_3O^+]=10^{-4.74}=1.8×10^{-5}\;M$$ $$mol\;H_3O^+=(0.100\;L)(1.8×10^{-5}\;M)=1.8×10^{-6}\;mol\;H_3O^+$$The amount of hydroxide ion added to the solution is
$$mol\;OH^-=(0.0010\;L)(0.10\;M)=1.0×10^{-4}\;mol\;OH^-$$The added hydroxide will neutralize hydronium ion via the reaction
$$H_3O^+\;(aq)+OH^-\;(aq)⇋2H_2O\;(l)$$The 1:1 stoichiometry of this reaction shows that an excess of hydroxide has been added (greater molar amount than the initially present hydronium ion).
The amount of hydroxide ion remaining is
$$1.0×10^{-4}\;mol-1.8×10^{-6}\;mol=9.8×10^{-5}\;mol\;OH^-$$corresponding to a hydroxide molarity of
$$\frac{9.8×10^{-5}\;mol}{0.101\;L}=9.7×10^{-4}\;M$$The pH of the solution is then calculated to be
$$\text{pH}=14.00-\text{pOH}=14.00–log(9.7×10^{-4})=10.99$$In this unbuffered solution, addition of the base results in a significant rise in pH (from 4.74 to 10.99) compared with the very slight increase observed for the buffer solution in part (b) (from 4.74 to 4.75).
Check Your Learning
Show that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a $1.8×10^{-5}\;M$ HCl solution from 4.74 to 3.00.
Answer:
Initial pH of $1.8×10^{-5}\;M$ HCl;
$\text{pH} = −log[H_3O^+] = −log[1.8×10^{−5}] = 4.74$ Moles of H3O+ in 100 mL $1.8×10^{-5}\;M$ HCl;
$1.8×10^{-5}\;\frac{moles}{L}\times 0.100\;L=1.8×10^{-6}$
Moles of $H_3O^+$ added by addition of 1.0 mL of 0.10 M HCl: $0.10\;moles/Lx0.0010L=1.0×10^{-4}$ moles;
final pH after addition of 1.0 mL of 0.10 M HCl: $$\text{pH}=-log[H_3O^+]=-log\left(\frac{\text{total moles }H_3O^+}{\text{total volume}}\right)=-log\left(\frac{1.0×10^{-4}\;mol+1.8×10^{-6}\;mol}{101\;mL\left(\frac{1\;L}{1000\;mL}\right)}\right)=3.00$$