Another common type of equilibrium calculation is one in which equilibrium concentrations are derived from initial concentrations and an equilibrium constant. For these calculations, a four-step approach is typically useful:
- Identify the direction in which the reaction will proceed to reach equilibrium.
(Compare Q and K) - Build an ICE table.
- Calculate the concentration changes and equilibrium concentrations.
- Confirm the calculated equilibrium concentrations.
The next two example exercises demonstrate the application of this strategy.
Calculation of Equilibrium Concentrations
Under certain conditions, the equilibrium constant $\mathit K_c$ for the decomposition of $PCl_5\mathit (g)$ into $PCl_3\mathit (g)$ and $Cl_2\, (g)$ is 0.0211. What are the equilibrium concentrations of $PCl_5$, $PCl_3$, and $Cl_2$ in a mixture that initially contained only $PCl_5$ at a concentration of 1.00 $\mathit M$
Solution
Use the stepwise process described earlier.
-
Identify the direction in which the reaction will proceed to reach equilibrium.
The balanced equation for the decomposition of $PCl_5$ is
$$PCl_5\;(g) ⇌ PCl_3\;(g) + Cl_2\;(g)$$Because only the reactant is present initially $\mathit {Q_c} = 0$ and the reaction will proceed to the right.
-
Develop an ICE table.
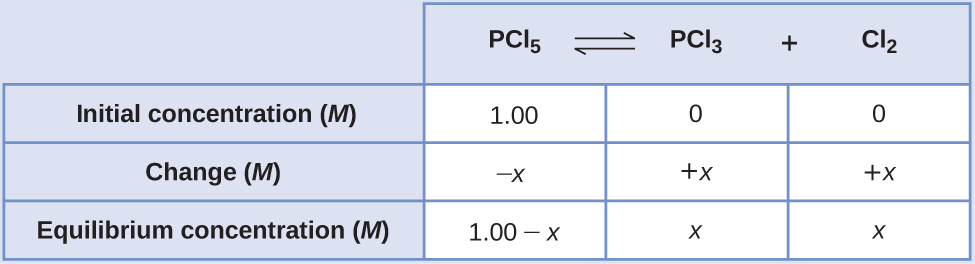
-
Solve for the change and the equilibrium concentrations.
Substituting the equilibrium concentrations into the equilibrium constant equation gives
$$K_c=\frac{[PCl_3][Cl_2]}{[PCl_5}\\ 0.0211=\frac{(x)(x)}{(1.00−x)}\\ 0.0211=\frac{(x)(x)}{(1.00−x)}\\ 0.0211(1.00−x)=x^2\\ x^2+0.0211x-0.0211=0$$We can use the quadratic equation to solve for $x$: see Appendix B for a refresher.
$$x=\frac{−b± \sqrt{b^2−4ac}}{2a}$$In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:
$$x=\frac{−0.0211± \sqrt{(0.0211)^2−4(1)(-0.0211)}}{(2)(1)}\\ x=\frac{−0.0211± \sqrt{(4.45×10^{-4})+(8.44×10^{-2})}}{2}\\ x=\frac{−0.0211±0.291}{2}$$ The two roots of the quadratic are: $$x=\frac{−0.0211+0.291}{2}=0.135$$ and $$x=\frac{−0.0211-0.291}{2}=−0.156$$ For this scenario, only the positive root is physically meaningful (concentrations are either zero or positive), and so $\mathbf{x = 0.135\, \text{M}}$.The equilibrium concentrations are
$$\mathbf{[PCl_5]=1.00-x=1.00−0.135=0.87\, \text{M}\\ [PCl_3]=x=0.135\, \text{M}\\ [Cl_2]=x=0.135\, \text{M}}$$ -
Confirm the calculated equilibrium concentrations.
Substitution into the expression for $K_c$ (to check the calculation) gives $$K_c=\frac{[PCl_3][Cl_2]}{[PCl_5]}\\ K_C=\frac{(0.135)(0.135)}{0.87}\\ K_C=0.021$$ The equilibrium constant calculated from the equilibrium concentrations is equal to the value of $K_c$ given in the problem (when rounded to the proper number of significant figures).
Check Your Learning
Acetic acid, $CH_3CO_2H$, reacts with ethanol, $C_2H_5OH$, to form water and ethyl acetate, $CH_3CO_2C_2H_5$.
$$CH_3CO_2H+C_2H_5OH \rightleftharpoons CH_3CO_2C_2H_5+H_2O$$The equilibrium constant $K_C$ for this reaction with dioxane as a solvent is 4.0. What are the equilibrium concentrations for a mixture that is initially 0.15 M in CH3CO2H, 0.15 M in C2H5OH, 0.40 M in CH3CO2C2H5, and 0.40 M in H2O?
Answer
Following the steps described above:
Identify the direction in which the reaction will proceed to reach equilibrium.
We can identify the direction of the reaction by calculating the reaction quotient Q: $$Q = \frac{[CH_3 CO_2 C_2 H_5][H_2 O]}{[CH_3 CO_2 H][C_2 H_5 OH]}\\ Q = \frac{[0.40\, \text{M}][0.40\, \text{M}]}{[0.15\, \text{M}][0.15\, \text{M}]}\\ Q = 7.111\\ Q \gt K: \text{the reaction will proceed to the left (towards the reactants)}$$ (Since the solvent is specified as dioxane, the water is not a solvent / pure liquid in this reaction and will appear in the equilibrium expression).
Develop an ICE table.
$CH_3CO_2H$ $+$ $C_2H_5OH $ $\rightleftharpoons $ $CH_3CO_2C_2H_5$ $+$ $H_2O$ Initial concentration 0.15 M 0.15 M 0.40 M 0.40 M Change in concentration +x +x -x -x Equilibrium concentration 0.15 + x 0.15 + x 0.40 – x 0.40 – x Calculate the concentration changes and the equilibrium concentrations.
Using the expression for K: $$ K = \frac{[CH_3 CO_2 C_2 H_5][H_2 O]}{[CH_3 CO_2 H][C_2 H_5 OH]}\\ 4.0 = \frac{[0.15+x][0.15+x]}{[0.40-x][0.40-x]}\\ 4.0 = \frac{[0.15+x]^2}{[0.40-x]^2}\\ \sqrt{4.0} = \sqrt{\frac{[0.15+x]^2}{[0.40-x]^2}}\\ \pm 2.0 = \frac{[0.15+x]}{[0.40-x]}\\ 0.80-2.0x = 0.15+x \;\&\; -0.80+2.0x = 0.15+x\\ x = 0.21_{667} \;\&\; 0.95$$ Only $x = 0.21_{667}$ makes chemical sense (the other value would result in a negative concentration if used). $$ [CH_3CO_2H] = [C_2H_5OH] = 0.15 + x = 0.36_{6667} = \mathbf{0.37\, \text{M}} \\ [CH_3CO_2C_2H_5] = [H_2 O] = 0.40 – x = 0.18_{3333} = \mathbf{0.18\, \text{M}}$$
Confirm the calculated equilibrium concentrations.
Sanity check: $$K = \frac{[CH_3 CO_2 C_2 H_5][H_2 O]}{[CH_3 CO_2 H][C_2 H_5 OH]}\\ K = \frac{[0.36_{6667}\, \text{M}][0.36_{6667}\, \text{M}]}{[0.18_{3333}\, \text{M}][0.18_{3333}\, \text{M}]}\\ K = 4.0$$ The recalculated K agrees with the provided (actual) K – our calculations are correct.
Check Your Learning
A 1.00-L flask is filled with 1.00 mole of H2 and 2.00 moles of I2. The value of the equilibrium constant $K_C$ for the reaction of hydrogen and iodine reacting to form hydrogen iodide is 50.5 under the given conditions. What are the equilibrium concentrations of H2, I2, and HI in moles/L?
$$H_2\;(g)+I_2\;(g)\rightleftharpoons 2\,HI\;(g)$$Answer
Following the steps described above:
No HI is present in this reaction ([HI] = 0). The reaction must proceed to the right (towards the products) in order to reach equilibrium.
$H_2$ $+$ $I_2 $ $\rightleftharpoons $ $2\, HI$ Initial concentration 1.00 M 2.00 M 0 M Change in concentration -x -x +2x Equilibrium concentration 1.00 – x 2.00 – x 2x -
Using the expression for K: $$ K = \frac{[HI]^2}{[H_2][I_2]}\\ 50.5 = \frac{[2x]^2}{[1.00-x][2.00-x]}\\ 46.5x^2 – 151.5x + 101 = 0 \\ \text{Solve using the quadratic formula:}\\ x = 0.934_{984} \;\&\; 2.32_{308}$$ Only $x = 0.934_{984}$ makes chemical sense (the other value would result in a negative concentration if used). $$[H_2] = 1.00 – x = 0.06_{5016} = \mathbf{0.07\, \text{M}}\\ [I_2] = 2.00 – x = 1.06_{5016} = \mathbf{1.07\, \text{M}}\\ [HI] = 2x = 1.86_{9968} = \mathbf{1.87\, \text{M}}\\$$
-
Sanity check: $$K = \frac{[HI]^2}{[H_2][I_2]}\\ K = \frac{[1.86_{9968}]^2}{[0.06_{5016}][1.06_{5016}]}\\ K = 50.5$$ The recalculated K agrees with the provided (actual) K – our calculations are correct.