If we fill a balloon with air and seal it, the balloon contains a specific amount of air at atmospheric pressure, let’s say 1 atm. If we put the balloon in a refrigerator, the gas inside gets cold and the balloon shrinks (although both the amount of gas and its pressure remain constant). If we make the balloon very cold, it will shrink a great deal, and it expands again when it warms up.
This video shows how cooling and heating a gas causes its volume to decrease or increase, respectively.
These examples of the effect of temperature on the volume of a given amount of a confined gas at constant pressure are true in general: The volume increases as the temperature increases, and decreases as the temperature decreases. Volume-temperature data for a 1-mole sample of methane gas at 1 atm are listed and graphed in [link].
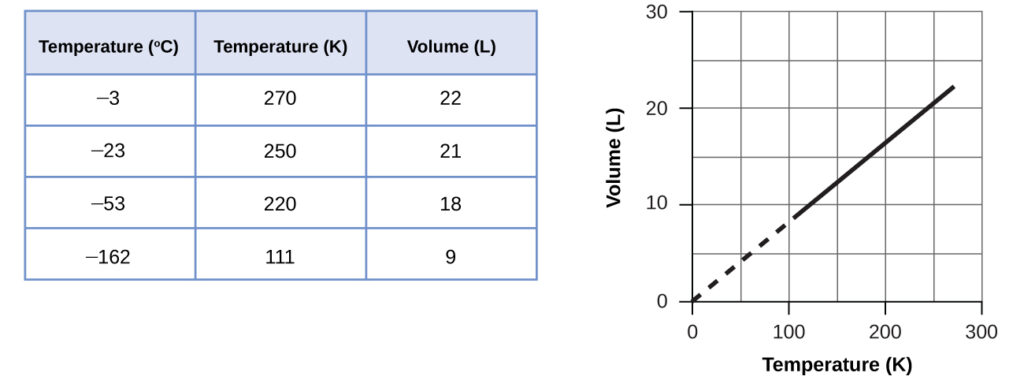
The relationship between the volume and temperature of a given amount of gas at constant pressure is known as Charles’s law in recognition of the French scientist and balloon flight pioneer Jacques Alexandre César Charles. Charles’s law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant.
Mathematically, this can be written as: $$V\;α\;T\quad or\quad V=constant·T\quad or\quad V=k·T\quad or\quad \frac{V_1}{T_1}=\frac{V_2}{T_2}$$
with k being a proportionality constant that depends on the amount and pressure of the gas.
For a confined, constant pressure gas sample, $\frac{V}{T}$ is constant (i.e., the ratio = k), and as seen with the P–T relationship, this leads to another form of Charles’s law: $\frac{V_1}{T_1}=\frac{V_2}{T_2}$.
Predicting Change in Volume with Temperature
A sample of carbon dioxide, CO2, occupies 0.300 L at 10 °C and 750 torr. What volume will the gas have at 30 °C and 750 torr?
Solution
Because we are looking for the volume change caused by a temperature change at constant pressure, this is a job for Charles’s law. Taking V1 and T1 as the initial values, T2 as the temperature at which the volume is unknown and V2 as the unknown volume, and converting °C into K we have: $$\frac{V_1}{T_1}=\frac{V_2}{T_2}\quad which\;means\; that\quad \frac{0.300\;L}{283\;K}=\frac{V_2}{303\;K}$$
Rearranging and solving gives: $$V_2=\frac{0.300\;L\times 303\;\require{enclose}\enclose{horizontalstrike}{K}}{283\; \enclose{horizontalstrike}{K}}=0.321\;L$$
This answer supports our expectation from Charles’s law, namely, that raising the gas temperature (from 283 K to 303 K) at a constant pressure will yield an increase in its volume (from 0.300 L to 0.321 L).
Check Your Learning
A sample of oxygen, O2, occupies 32.2 mL at 30 °C and 452 torr. What volume will it occupy at –70 °C and the same pressure?
Answer:
21.6 mL
Measuring Temperature with a Volume Change
Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales.
Solution
A volume change caused by a temperature change at constant pressure means we should use Charles’s law. Taking V1 and T1 as the initial values, T2 as the temperature at which the volume is unknown and V2 as the unknown volume, and converting °C into K we have:
$$\frac{V_1}{T_1}=\frac{V_2}{T_2}\quad which\;means\;that\quad \frac{150.0\;cm^3}{273.15\;K}=131.7\;cm^3$$
Rearrangement gives $$T2=\frac{131.7\;\enclose{horizontalstrike}{cm^3}\times 273.15\;K}{150.0\;\enclose{horizontalstrike}{cm^3}}=239.8\;K$$
Subtracting 273.15 from 239.8 K, we find that the temperature of the boiling ammonia on the Celsius scale is –33.4 °C.
Check Your Learning
What is the volume of a sample of ethane at 467 K and 1.1 atm if it occupies 405 mL at 298 K and 1.1 atm?
Answer:
635 mL