The equilibrium constant for a reaction is calculated from the equilibrium concentrations (or pressures) of its reactants and products. If these concentrations are known, the calculation simply involves their substitution into the K expression, as was illustrated by this previous example.
More often, we will know the value of an equilibrium constant and want to predict the equilibrium concentrations of reactants or products. This type of calculation is helpful for many types of equilibrium computations and relies on the use of terms for the reactant and product concentrations initially present, for how they change as the reaction proceeds, and for what they are when the system reaches equilibrium. The acronym ICE is commonly used to refer to this mathematical approach, and the concentrations terms are usually gathered in a tabular format called an ICE table.
Calculation of an Equilibrium Constant
Iodine molecules react reversibly with iodide ions to produce triiodide ions.
If a solution with the concentrations of I2 and I− both equal to $1.000×10^{−3}\mathit M$ before reaction gives an equilibrium concentration of I2 of $6.61×10^{−4}\mathit M$, what is the equilibrium constant for the reaction?
Solution
To calculate the equilibrium constants, equilibrium concentrations are needed for all the reactants and products:
$$K_c=\frac{[I_3^-]}{[I_2][I^-]}$$
Provided are the initial concentrations of the reactants and the equilibrium concentration of the product. Use this information to derive terms for the equilibrium concentrations of the reactants, presenting all the information in an ICE table.
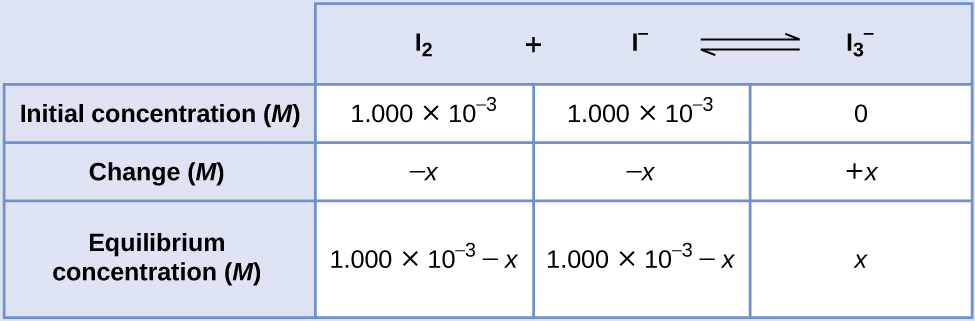
At equilibrium the concentration of I2 is $6.61×10^{−4}\mathit M$ so that $$1.000×10^{-3}-x=6.61×10^{-4}\\ x=1.000×10^{-3}-6.61×10^{-4}\\ x =3.39×10^{-4}$$
The ICE table may now be updated with numerical values for all its concentrations:

Finally, substitute the equilibrium concentrations into the K expression and solve:
$$K_C=\frac{[I_3^-]}{[I_2][I^-]}\\ K_C=\frac{3.39×10^{-4}\;M}{(6.61×10^{-4}\;M)(6.61×10^{-4}\;M)}\\ K_C= 776$$Check Your Learning
Ethanol and acetic acid react and form water and ethyl acetate, the solvent responsible for the odor of some nail polish removers. $$C_2H_5OH+CH_3CO_2H \rightleftharpoons CH_3CO_2C_2H_5+H_2O$$ When 1.00 mol each of C2H5OH and CH3CO2H are allowed to react in 1.00 L of the solvent dioxane, equilibrium is established when 0.333 mol of each of the reactants remains. Calculate the equilibrium constant for the reaction. (Note: Water is a solute in this reaction, not a solvent / liquid.)
Answer
First, set up your ICE table:
| $C_2H_5OH$ | + | $CH_3CO_2H$ | $\rightleftharpoons$ | $CH_3CO_2C_2H_5$ | + | $H_2O$ | |
| Initial Concentration | $\frac{1.00\,\text{mol}}{1.00\,\text{L}}$ | $\frac{1.00\,\text{mol}}{1.00\,\text{L}}$ | $0$ | <$0$ | |||
| Change (M) | $-x$ | $-x$ | $+x$ | <$+x$ | |||
| Final Concentration (M) | $\frac{0.333\,\text{mol}}{1.00\,\text{L}}$ | $\frac{0.333\,\text{mol}}{1.00\,\text{L}}$ | $x$ | <$x$ |
From this table, we can calculate the “change” value and final concentrations for the remaining species: $$\frac{1.00\,\text{mol}}{1.00\,\text{L}} – \frac{x\,\text{mol}}{1.00\,\text{L}} = \frac{0.333\,\text{mol}}{1.00\,\text{L}} \\ x = 0.667\, \frac{\text{mol}}{\text{L}}\\ [CH_3CO_2C_2H_5] = [H_2O] = 0.667\, \text{M} $$ Then, use our equilibrium concentrations to find K: $$ K_C = \frac{[CH_3CO_2C_2H_5][H_2O]}{[C_2H_5OH][CH_3CO_2H]} \\ K_C = \frac{[0.667\, \text{M}][0.667\, \text{M}]}{[0.333\, \text{M}][0.333\, \text{M}]} \\ \mathbf{K_C = 4.01} $$