Pressure and n

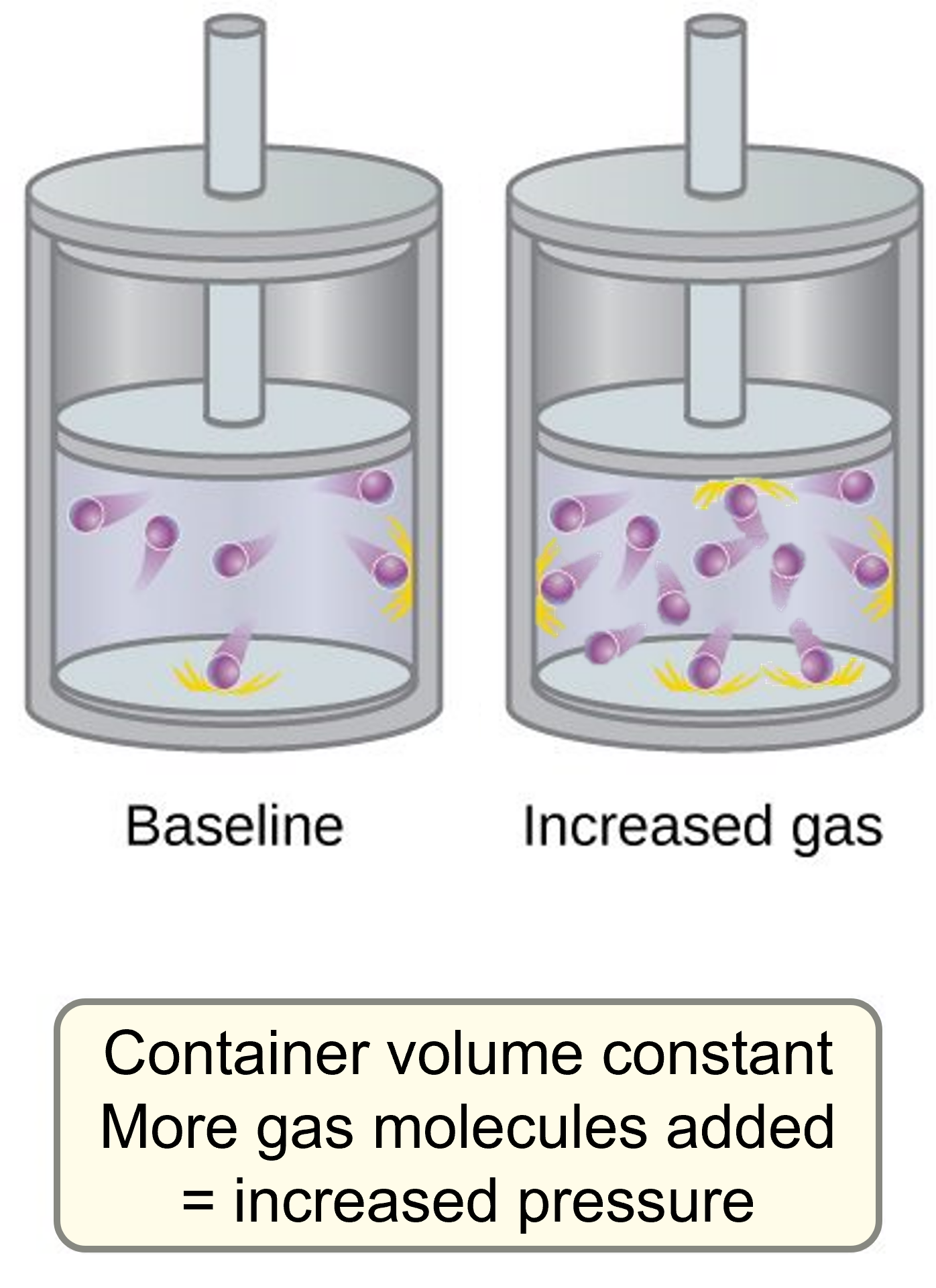
When we add more gas (increasing the n or number of moles of gas in the container), there are now more particles of gas in the container, colliding with the walls. Although we have not changed the force applied with each collision, the number of collisions with the walls has increased. This causes the pressure in the container to increase.

This figure shows a pair of pistons and cylinders. the piston is positioned for the first cylinder so that just over half of the available volume contains 6 purple spheres with trails behind them. The trails indicate movement. Orange dashes extend from the interior surface of the cylinder where the spheres have collided. This cylinder is labeled, “Baseline.” In the second cylinder, the number of purple spheres has changed from 6 to 12 and pressure, indicated by the number of collisions has doubled. This second cylinder is labeled “Increased gas.” A rectangle beneath the diagram states, “At constant volume, More gas molecules added equals Increased pressure.”
When the amount of gas increases at a constant volume, pressure increases due to the increased number of collisions per unit wall area per unit time.

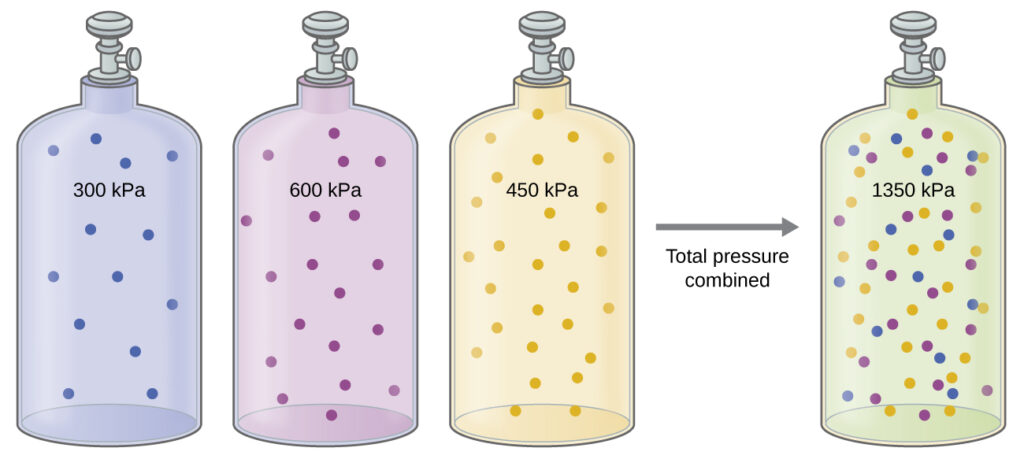
Partial Pressures

This direct relation between number of moles and pressure also explains the concept of partial pressures of gases in a mixture: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases: $$P_{Total}=P_A+P_B+P_C+…=\sum_{i}P_i$$

In the equation PTotal is the total pressure of a mixture of gases, PA is the partial pressure of gas A; PB is the partial pressure of gas B; PC is the partial pressure of gas C; and so on. This works because of our assumption #4 in the definition of kinetic molecular theory: the gas particles do not interact with each other, so it doesn’t matter if we have 1 mol of A and 1 mol of B; or 2 mol of A – all (ideal) gas particles behave in the same way, and only the total amount matters.

This figure includes images of four gas-filled cylinders or tanks. Each has a valve at the top. The interior of the first cylinder is shaded blue. This region contains 5 small blue circles that are evenly distributed. The label “300 k P a” is on the cylinder. The second cylinder is shaded lavender. This region contains 8 small purple circles that are evenly distributed. The label “450 k P a” is on the cylinder. To the right of these cylinders is a third cylinder. Its interior is shaded pale yellow. This region contains 12 small yellow circles that are evenly distributed. The label “6000 k P a” is on this region of the cylinder. An arrow labeled “Total pressure combined” appears to the right of these three cylinders. This arrow points to a fourth cylinder. The interior of this cylinder is shaded a pale green. It contains evenly distributed small circles in the following quantities and colors; 5 blue, 8 purple, and 12 yellow. This cylinder is labeled “1350 k P a.”
If equal-volume cylinders containing gas A at a pressure of 300 kPa, gas B at a pressure of 600 kPa, and gas C at a pressure of 450 kPa are all combined in the same-size cylinder, the total pressure of the mixture is 1350 kPa.

The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction (X), a unit of concentration defined as the number of moles of a component of a solution divided by the total number of moles of all components:

$$P_A=X_A×P_{Total}\qquad where\qquad X_A=\frac{n_A}{n_{Total}}$$

where PA, XA, and nA are the partial pressure, mole fraction, and number of moles of gas A, respectively, and nTotal is the number of moles of all components in the mixture.

The Pressure of a Mixture of Gases

A 10.0-L vessel contains 2.50 ×10−3 mol of H2, 1.00 ×10−3 mol of He, and 3.00 ×10−4 mol of Ne at 35 °C.

(a) What are the partial pressures of each of the gases, in bar?

(b) What is the total pressure in bar?

Solution

The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using $$P=\frac{nRT}{V}\\ P_{H_2}=\frac{(2.50×10^{−3}\;\require{enclose}\enclose{horizontalstrike}{mol})(0.08314510\; \enclose{horizontalstrike}{L}\;bar\; \enclose{horizontalstrike}{mol^{-1}K^{−1}})(308\; \enclose{horizontalstrike}{K})}{10.0\; \enclose{horizontalstrike} {L}}=6.40×10^{−3}\;bar\\ P_{He}= \frac{(1.00×10^{−3}\;\enclose{horizontalstrike}{mol})(0.08314510\; \enclose{horizontalstrike}{L}\;bar\; \enclose{horizontalstrike}{mol^{-1}K^{−1}})(308\; \enclose{horizontalstrike}{K})}{10.0\; \enclose{horizontalstrike} {L}}=2.56×10^{−3}\;bar\\P_{Ne}=\frac{(3.00×10^{−4}\;\enclose{horizontalstrike}{mol})(0.08314510\; \enclose{horizontalstrike}{L}\;bar\; \enclose{horizontalstrike}{mol^{-1}K^{−1}})(308\; \enclose{horizontalstrike}{K})}{10.0\; \enclose{horizontalstrike} {L}}=7.68×10^{−4}\;bar$$

The total pressure is given by the sum of the partial pressures:

$$P_T=P_{H_2}+P_{He}+P_{Ne}=(0.00640+0.00256+0.000768)\;bar=0.00972_{8}\; bar=\mathbf{9.73×10^{−3}\;bar}$$

Check Your Learning

A 5.73-L flask at 25 °C contains 0.0388 mol of N2, 0.147 mol of CO, and 0.0803 mol of H2. What is the total pressure in the flask in atmospheres?

Answer

1.137 atm

Here is another example of this concept, but dealing with mole fraction calculations.

The Pressure of a Mixture of Gases

A gas mixture used for anesthesia contains 2.83 mol oxygen, O2, and 8.41 mol nitrous oxide, N2O. The total pressure of the mixture is 192 kPa.

(a) What are the mole fractions of O2 and N2O?

(b) What are the partial pressures of O2 and N2O?

Solution

The mole fraction is given by $X_A=\frac{n_A}{n_{total}}$ and the partial pressure is $P_A = X_A \times P_{total}$ .

For O2,

$$X_{O_2}=\frac{n_{O_2}}{n_{total}}=\frac{2.83\;mol}{(2.83+8.41)\;mol}=0.252 \\ P_{O_2}=X_{O_2}\times P_{total}=0.252\times 192\;kPa=48.4\;kPa$$

For N2O,

$$X_{N_2O}=\frac{n_{N_2O}}{n_{total}}=\frac{8.41\;mol}{(2.83+8.41)\;mol}=0.748 \\ P_{N_2O}=X _{N_2O} \times P_{total}=0.748\times 192\;kPa=143.6\;kPa$$

Check Your Learning

What is the pressure (in bar) of a mixture of 0.200 g of H2, 1.00 g of N2, and 0.820 g of Ar in a container with a volume of 2.00 L at 20 °C?

Answer

1.89 bar