The identity of a substance is defined not only by the types of atoms or ions it contains but by the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, sophisticated instruments allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for the amount of substances, the mole, which remains indispensable in modern chemical science.
The mole is an amount unit similar to familiar units like pair, dozen, etc. It provides a specific measure of the number of atoms or molecules in a sample of matter. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth.
A mole of substance is that amount in which there are 6.02214076 × 1023 discrete entities (atoms or molecules). This large number is a fundamental constant known as Avogadro’s number (NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022 × 1023/mol.
Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol). In the figure below, each element sample contains about 1 mol of that element – notice the mass of each.

The molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). A mole of 12C weighs 12 g (its molar mass is 12 g/mol). This relationship holds for all elements since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu.

While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g. Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

The mole is used in chemistry to represent 6.022 × 1023 of something, but it can be difficult to conceptualize such a large number. Watch this video and complete the “Think” questions that follow. Explore more about the mole by reviewing the information under “Dig Deeper”.
The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds, as demonstrated in the next several example problems.
Deriving Moles from Grams for an Element
According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?
Solution
The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.
The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

The unit analysis method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:” $$4.7\,g\,K\,\left(\frac{\text{mol}\,K}{39.10\,g\,K}\right)\,=\,0.12\,\text{mol}\,K$$
The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation since it is a bit greater than 0.1 mol.
Check Your Learning
Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?
Answer:
0.360 mol
Deriving Grams from Moles for an Element
A liter of air contains 9.2 × 10−4 mol argon. What is the mass of Ar in a liter of air?
Solution
The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

In this case, logic dictates (and the unit analysis method supports) multiplying the provided amount (mol) by the molar mass (g/mol): $$9.2\,×\,10^{−4}\,\text{mol}\,Ar\left(\frac{39.95\,g}{\text{mol}\,Ar}\right)=0.037g\,Ar$$
The result is in agreement with our expectations, around 0.04 g Ar.
Check Your Learning
What is the mass of 2.561 mol of gold?
Answer
504.4 g
Deriving Number of Atoms from Mass for an Element
Copper is commonly used to fabricate electrical wire. How many copper atoms are in 5.00 g of copper wire?

Solution
The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to the number of Cu atoms:

Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:
$$5.00\,g\,Cu \left(\frac{\text{mol}\,Cu}{63.55\,g\,Cu}\right) \left(\frac{6.022\,×\,10^{23}\text{Cu atoms}}{\text{mol}\,Cu}\right)\\
=\,4.74\,×\,10^{22}\,\text{Cu atoms}$$
The unit analysis method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.
Check Your Learning
A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?
Answer
4.586 × 1022 Au atoms
Deriving Moles from Grams for a Compound
Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula $C_2H_5O_2N$. How many moles of glycine molecules are contained in 28.35 g of glycine?
Solution
Derive the number of moles of a compound from its mass following the same procedure used for an element:
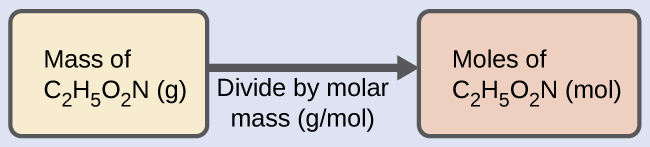
The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, $C_2H_5O_2N$, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:
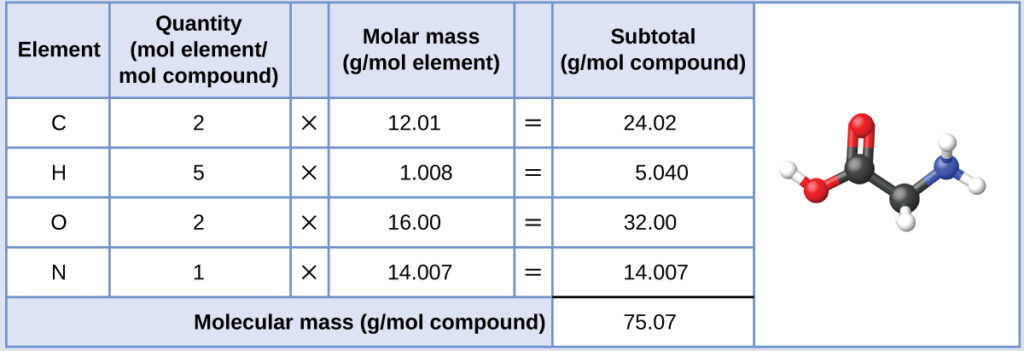
The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so the computed result is expected to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields: $$28.35\,\text{g glycine}\left(\frac{\text{mol glycine}}{75.07\,\text{g glycine}}\right)=\,0.378\,\text{mol glycine}$$ This result is consistent with the rough estimate.
Check Your Learning
How many moles of sucrose, $C_{12}H_{22}O_{11}$, are in a 25 g sample of sucrose?
Answer
0.073 mol
Deriving Grams from Moles for a Compound
Vitamin C is a covalent compound with the molecular formula C_6H_8O_6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?
Solution
As for elements, the mass of a compound can be derived from its molar amount as shown:

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, the corresponding mass is expected to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation yields: $$1.42\,×\,10^{−4}\,\text{mol vitamin C}\left(\frac{176.124\,\text{g vitamin C}}{\text{mol vitamin C}}\right)=\,0.0250\,\text{g vitamin C}$$
This is consistent with the anticipated result.
Check Your Learning
What is the mass of 0.443 mol of hydrazine, $N_2H_4$?
Answer
14.2 g
Deriving the Number of Atoms and Molecules from the Mass of a Compound
A packet of an artificial sweetener contains 40.0 mg of saccharin ($C_7H_5NO_3S$), which has the structural formula:
Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?
Solution
The number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated below, and then multiplying by Avogadro’s number:

Using the provided mass and molar mass for saccharin yields: $$0.0400\,g\,C_7H_5NO_3S\left(\frac{\text{mol}\,C_7H_5NO_3S}{183.18\,g\,C_7H_5NO_3S}\right)\left(\frac{6.022\,×\,10^{23}\,C_7H_5NO_3S\,\text{molecules}}{1\,\text{mol}\,C_7H_5NO_3S}\right)\\
=\,1.31\,×\,10^{20}\,C_7H_5NO_3S\,\text{molecules}$$
The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is: $$1.31\,×\,10^{20}\,C_7H_5NO_3S\,\text{molecules}\left(\frac{7\,C\,\text{atoms}}{1\,C_7H_5NO_3S\,\text{molecule}}\right)=\,9.17\,×\,10^{20}\,C\,\text{atoms}$$
Check Your Learning
How many $C_4H_{10}$ molecules are contained in 9.213 g of this compound? How many hydrogen atoms?
Answer
Answer
9.545 × 1022 molecules $C_4 H_{10}$
9.545 × 1023 atoms H
Counting Neurotransmitter Molecules in the Brain
The brain is the control center of the central nervous system. It sends and receives signals to and from muscles and other internal organs to monitor and control their functions; it processes stimuli detected by sensory organs to guide interactions with the external world; and it houses the complex physiological processes that give rise to our intellect and emotions. The broad field of neuroscience spans all aspects of the structure and function of the central nervous system, including research on the anatomy and physiology of the brain. Great progress has been made in brain research over the past few decades, and the BRAIN Initiative, a federal initiative announced in 2013, aims to accelerate and capitalize on these advances through the concerted efforts of various industrial, academic, and government agencies.
Specialized cells called neurons transmit information between different parts of the central nervous system by way of electrical and chemical signals. Chemical signaling occurs at the interface between different neurons when one of the cells releases molecules (called neurotransmitters) that diffuse across the small gap between the cells (called the synapse) and bind to the surface of the other cell. These neurotransmitter molecules are stored in small intracellular structures called vesicles that fuse to the cell wall and then break open to release their contents when the neuron is appropriately stimulated. This process is called exocytosis (see figure below). One neurotransmitter that has been very extensively studied is dopamine, $C_8H_{11}NO_2$. Dopamine is involved in various neurological processes that impact a wide variety of human behaviors. Dysfunctions in the dopamine systems of the brain underlie serious neurological diseases such as Parkinson’s and schizophrenia.
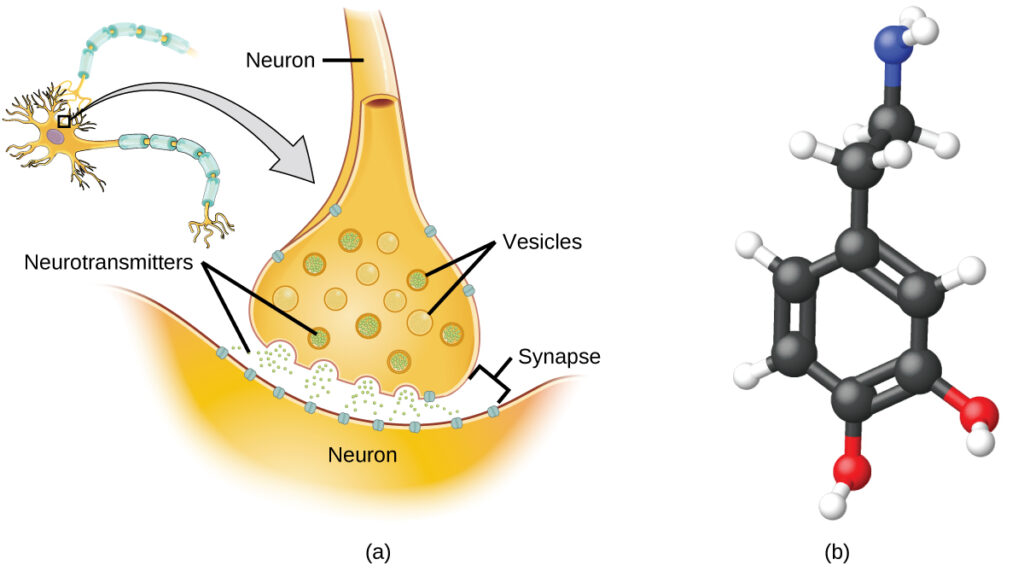
One important aspect of the complex processes related to dopamine signaling is the number of neurotransmitter molecules released during exocytosis. Since this number is a central factor in determining neurological response (and subsequent human thought and action), it is important to know how this number changes with certain controlled stimulations, such as the administration of drugs. It is also important to understand the mechanism responsible for any changes in the number of neurotransmitter molecules released—for example, some dysfunction in exocytosis, a change in the number of vesicles in the neuron, or a change in the number of neurotransmitter molecules in each vesicle.
Significant progress has been made recently in directly measuring the number of dopamine molecules stored in individual vesicles and the amount actually released when the vesicle undergoes exocytosis. Using miniaturized probes that can selectively detect dopamine molecules in very small amounts, scientists have determined that the vesicles of a certain type of mouse brain neuron contain an average of 30,000 dopamine molecules per vesicle (about 5 × 10−20 mol or 50 zmol). Analysis of these neurons from mice subjected to various drug therapies shows significant changes in the average number of dopamine molecules contained in individual vesicles, increasing or decreasing by up to three-fold, depending on the specific drug used. These studies also indicate that not all of the dopamine in a given vesicle is released during exocytosis, suggesting that it may be possible to regulate the fraction released using pharmaceutical therapies.1
Footnotes
- 1 Omiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447.