Objectives
By the end of this section, you will be able to:
- Describe the Bohr model of the hydrogen atom
- Use the Rydberg equation to calculate energies of light emitted or absorbed by hydrogen atoms
After Ernest Rutherford, and his team’s work in the early 20th century, scientist stated that atoms have a dense nucleus surrounded by tiny, fast-moving electrons. This model, the planetary model, likens to a miniature “solar system”; electrons orbit the nucleus like planets orbit the sun.
The simplest atom is hydrogen, a single proton as the nucleus and a single electron orbits it. The electrostatic force attracting the electron to the proton depends only on how apart they are.
However, this classical mechanics description of the atom is incomplete. An electron moving in an elliptical orbit would be accelerating (by changing direction). According to classical electromagnetism, it should continuously emit electromagnetic radiation. This would cause the electrons orbit to shrink it spirals into the nucleus, suggesting that atoms are inherently unstable.
Neils Bohr
In 1913, Niels Bohr addressed the atomic paradox. He ignored classical electromagnetism’s prediction that the orbiting electron in hydrogen would continuously emit light. Instead, he incorporated into the classical mechanics description of the atom Planck’s ideas of quantization and Einstein’s finding. Einsteins findings, photon theory) stated that light consists of photons whose energy is proportional to their frequency. Bohr assumed that the electron orbiting the nucleus would not normally emit any radiation (the stationary state hypothesis). On the contrary, it would emit or absorb a photon if it moved to a different orbit. The energy absorbed or emitted would reflect differences in the orbital energies according to this equation:
$$|ΔE|=|E_f-E_i|=hv=\frac{hc}{λ}$$The equation, h is Planck’s constant and Ei and Ef are the initial and final orbital energies, respectively. Scientist use the absolute value of the energy difference because frequencies and wavelengths are always positive. Instead of allowing for continuous values of energy, Bohr assumed the energies of these electron orbitals were quantized:
$$E_n=-\frac{k}{n^2},\;n=1,\;2,\;3,\;.\;.\;.$$In this expression, k is a constant comprising fundamental constants such as the electron mass and charge and Planck’s constant. Inserting the expression for the orbit energies into the equation for ΔE gives
$$ΔE=k(\frac{1}{n_1^2}-\frac{1}{n_2^2})=\frac{hc}{λ}$$or
$$\frac{1}{λ}=\frac{k}{hc}(\frac{1}{n_1^2}-\frac{1}{n_2^2})$$which is identical to the Rydberg equation in which $R_∞=\frac{k}{hc}$. When Bohr calculated his theoretical value for the Rydberg constant, $R_∞$. He later compared it with the experimentally accepted value, he got excellent agreement. Since the Rydberg constant was one of the most precisely measured constants, at that time, this level of agreement was astonishing and made people take Bohr’s model seriously, despite the many assumptions Bohr used to develop it.
Ground State and Excited State
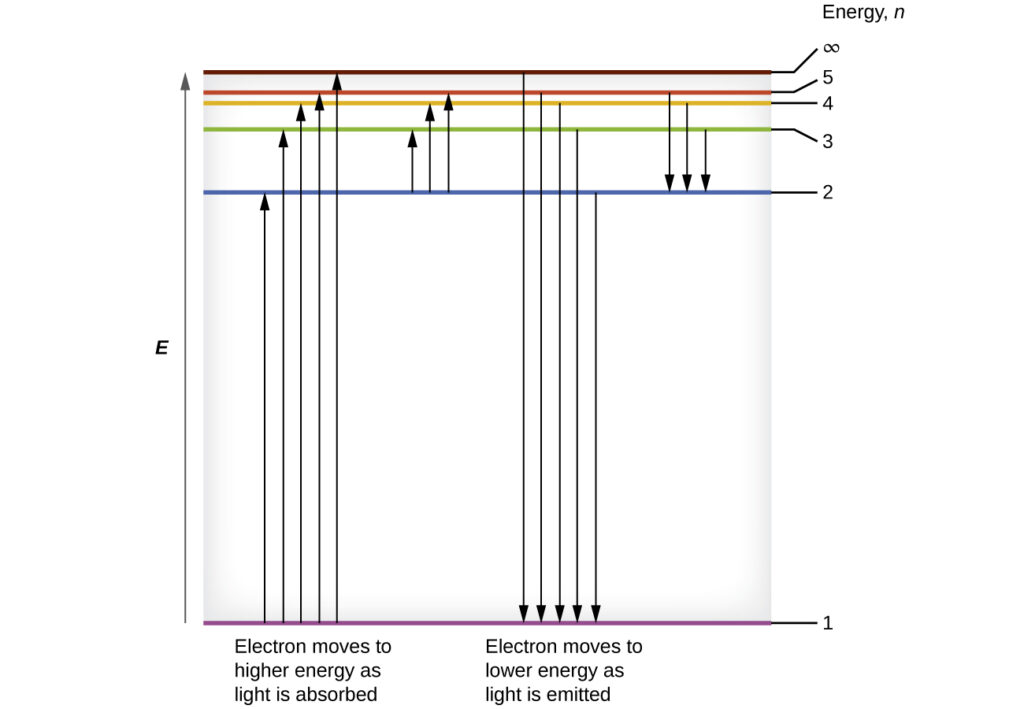
Figure 1 below shows the lowest few energy levels. One of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n = 1 orbit, the orbit in which it has the lowest energy. When the electron is in this lowest energy orbit, the atom is in its ground electronic state (or simply ground state). If the atom receives energy from an outside source, it is possible for the electron to move to an orbit with a higher n value and the atom is now in an excited electronic state (or simply an excited state) with a higher energy. When an electron moves from an excited state (higher energy orbit) to a less excited state, or ground state, it emits the energy difference as a photon.
Similarly, when an atom absorbs a photon, the energy of the photon moves an electron from a lower energy orbit up to a more excited one. We can relate the energy of electrons in atoms to what we learned previously about energy. The law of conservation of energy says that we can neither create nor destroy energy. When enough external energy is provided, the electron is excited from one energy level to another. The electron will release the same amount of energy when it returns to its initial state. This energy can be though as ‘liberated’ or ‘free’ when the electron returns to its initial state.
Nuclear Charge
Since Bohr’s model involved only a single electron, scientist applied it to single-electron ions like He+, Li2+, Be3+. These ions differ from hydrogen only in their nuclear charges, so scientist refer to one-electron atoms and ions are collectively as hydrogen-like atoms. The energy expression for hydrogen-like atoms is a generalization of the hydrogen atom energy, in which Z is the nuclear charge (+1 for hydrogen, +2 for He, +3 for Li, and so on) and k has a value of 2.179 10–18 J.
$$E_n=-\frac{kZ^2}{n^2}$$Energy and Distance Relationship in Electron Orbitals
The expression beow gives the sizes of the circular orbits for hydrogen-like atoms in terms of their radii . Here, $α_0$ is Bohr radius, a constant with a value of $5.292×10^{−11}$ m:
$$r=\frac{n^2}{Z}a_0$$The equation also shows us that as the electron’s energy increases (as n increases), the electron is farther away from the nucleus, implied by the inverse dependence of electrostatic attraction on distance. The relationship shows that as electron moves away from the nucleus, the electrostatic attraction between them decreases. This decrease leads to the electrons having less hold within the atom. As n and the orbits increase, their energies approach zero. Thus, the limits and , E = 0 marks the ionization limit where the electron is fully removed from the nucleus. Thus, for hydrogen in the ground state n = 1, the ionization energy would be:
$$ΔE=E_{n⟶∞}-E_1=0+k=k$$Bohr’s Model and Quantum Mechanics
Solving three major paradoxes – blackbody radiation, the photoelectric effect, and the hydrogen atom – and all involving Planck’s constant showed physicists, at that time, that the classical theories, effective in the macroscopic world were fundamentally flawed. These theories could not extended to the microscopic domain of atoms and molecules. Unfortunately, despite Bohr’s remarkable achievement in deriving a theoretical expression for the Rydberg constant, he was unable to extend his theory to the next simplest atom, He, which only has two electrons. Bohr’s model was severely flawed, because it relied on the classical mechanics concept of precise orbits. This idea proved untenable in the microscopic domain when a proper model of quantum mechanics was developed to supersede classical mechanics.

Calculating the Energy of an Electron in a Bohr Orbit
Early researchers were very excited when they were able to predict the energy of an electron at a particular distance from the nucleus in a hydrogen atom. If a spark promotes the electron in a hydrogen atom into an orbit with n = 3, what is the calculated energy, in joules, of the electron?
Solution
The energy of the electron is given by this equation:
$$E_n=-\frac{kZ^2}{n^2}$$
The atomic number, $Z$, of hydrogen is 1; $k= 2.179×10^{–18}\;J$; and the electron is characterized by an $n$ value of 3. Thus, $$E=\frac{-(2.179×10^{-18})\times (1)^2}{(3)^2}=-2.421×10^{-19}\;J$$
Check Your Learning
The electron is promoted even further to an orbit with n = 6. What is its new energy?
$−6.053×10^{-20}\;J$
Calculating the Energy and Wavelength of Electron Transitions in a One–electron (Bohr) System
What is the energy (in joules) and the wavelength (in meters) of the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 4 to the orbit with n = 6? In what part of the electromagnetic spectrum do we find this radiation?
Solution
In this case, the electron starts out with n = 4, so n1 = 4. It comes to rest in the n = 6 orbit, so n2 = 6. The difference in energy between the two states is given by this expression:
This energy difference is positive, indicating a photon enters the system (is absorbed) to excite the electron from the n = 4 orbit up to the n = 6 orbit. The wavelength of a photon with this energy is found by the expression $E=\frac{hc}{λ}$. Rearrangement gives:
$$λ=\frac{hc}{E}$$ $$λ=(6.626×10^{-34}\;\require{enclose}\enclose{horizontalstrike}{J\;s})\times\frac{2.998×10^8\;m\enclose{horizontalstrike}{s^{-1}}}{7.566×10^{-20}\;\enclose{horizontalstrike}{J}}$$ $$λ=2.626×10^{-6}\;m$$From the illustration of the electromagnetic spectrum in Electromagnetic Energy, we can see that this wavelength is found in the infrared portion of the electromagnetic spectrum.
Check Your Learning
What is the energy in joules and the wavelength in meters of the photon produced when an electron falls from the n = 5 to the n = 3 level in a He+ ion (Z = 2 for He+)?
$6.198×10^{–19}\;J$; $3.205×10^{−7}\;m$
Bohrs Model Insights and Limitations
Bohr’s hydrogen atom model provides insight into the behavior of matter at the microscopic level. However, it is does not account for electron–electron interactions in atoms with more than one electron. It does introduce several important features of all models used to describe the distribution of electrons in an atom. These features include the following:
- Electron’s energy levels in an atom are quantized, described by quantum numbers.
- Integer numbers have specific allowed value and used to characterize the arrangement of electrons in an atom.
- An electron’s energy increases with increasing distance from the nucleus.
- The discrete energies (lines) in the spectra of the elements result from quantized electronic energies.
Of these features, the most important is the postulate of quantized energy levels for an electron in an atom. As a consequence, the model laid the foundation for the quantum mechanical model of the atom. Bohr won a Nobel Prize in Physics for his contributions to our understanding of the structure of atoms and how that is related to line spectra emissions.
Key Concepts and Summary
Bohr incorporated Planck’s and Einstein’s quantization ideas into a model of the hydrogen atom that resolved the paradox of atom stability and discrete spectra. The Bohr model of the hydrogen atom explains the connection between the quantization of photons and the quantized emission from atoms. Bohr described the hydrogen atom in terms of an electron moving in a circular orbit about a nucleus. He postulated that the electron was restricted to certain orbits characterized by discrete energies. Transitions between these allowed orbits result in the absorption or emission of photons. When an electron moves from a higher-energy orbit to a more stable one, energy is emitted in the form of a photon. To move an electron from a stable orbit to a more excited one, a photon of energy must be absorbed. Using the Bohr model, we can calculate the energy of an electron and the radius of its orbit in any one-electron system.