Key Concepts and Summary
Gibbs free energy (G) is a state function defined with regard to system quantities only and may be used to predict the spontaneity of a process. A negative value for ΔG indicates a spontaneous process; a positive ΔG indicates a nonspontaneous process; and a ΔG of zero indicates that the system is at equilibrium. A number of approaches to the computation of free energy changes are possible.
Key Equations
| ΔG = ΔH − TΔS |
Practice Problems
What is the difference between ΔG and ΔG° for a chemical change?
A reaction has $\Delta H^\circ= 100\; kJ/mol$ and $\Delta S^\circ = 250\; J/mol \cdot K$
Is the reaction spontaneous at room temperature? If not, under what temperature conditions will it become spontaneous?
Solution
The reaction is nonspontaneous at room temperature.
Above 400 K, ΔG will become negative, and the reaction will become spontaneous.
Explain what happens as a reaction starts with ΔG < 0 (negative) and reaches the point where ΔG = 0.
Use the standard free energy of formation data in Appendix to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.
(a)
(b)
(c)
(d)
(e)
(f)
Solution
(a) 465.1 kJ nonspontaneous;
(b) −106.86 kJ spontaneous;
(c) −291.9 kJ spontaneous;
(d) −83.4 kJ spontaneous;
(e) −406.7 kJ spontaneous;
(f) −30.0 kJ spontaneous
Use the standard free energy data in Appendix to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.
(a)
(b)
(c)
(d)
(e)
(f)
Given:
(a) Determine the standard free energy of formation, for phosphoric acid.
(b) How does your calculated result compare to the value in Appendix? Explain.
Solution
(a) The standard free energy of formation is –1124.3 kJ/mol.
(b) The calculation agrees with the value in Appendix because free energy is a state function (just like the enthalpy and entropy), so its change depends only on the initial and final states, not the path between them.
Is the formation of ozone (O3(g)) from oxygen (O2(g)) spontaneous at room temperature under standard state conditions?
Consider the decomposition of red mercury(II) oxide under standard state conditions.
(a) Is the decomposition spontaneous under standard state conditions?
(b) Above what temperature does the reaction become spontaneous?
Solution
(a) The reaction is nonspontaneous;
(b) Above 566 °C the process is spontaneous.
Among other things, an ideal fuel for the control thrusters of a space vehicle should decompose in a spontaneous exothermic reaction when exposed to the appropriate catalyst. Evaluate the following substances under standard state conditions as suitable candidates for fuels.
(a) Ammonia:
(b) Diborane:
(c) Hydrazine:
(d) Hydrogen peroxide:
Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.
(a)
(b)
(c)
(d)
(e)
(f)
Solution
(a) 1.5×102 kJ; (b) −21.9 kJ; (c) −5.34 kJ; (d) −0.383 kJ; (e) 18 kJ; (f) 71 kJ
Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.
(a)
(b)
(c)
(d)
(e)
(f)
Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.
(a)
(b)
(c)
(d)
(e)
Solution
(a) K = 41; (b) K = 0.053; (c) K = 6.9 1013; (d) K = 1.9; (e) K = 0.04
Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.
(a)
(b)
(c)
(d)
(e)
Calculate the equilibrium constant at the temperature given.
(a)
(b)
(c)
(d)
(e)
Solution
In each of the following, the value of ΔG is not given at the temperature of the reaction. Therefore, we must calculate ΔG from the values ΔH° and ΔS and then calculate ΔG from the relation ΔG = ΔH° − TΔS°.
(a) K = 1.29;
(b) K = 2.51
10−3;
(c) K = 4.83
103;
(d) K = 0.219;
(e) K = 16.1
Calculate the equilibrium constant at the temperature given.
(a)
(b)
(c)
(d)
(e)
Consider the following reaction at 298 K:
What is the standard free energy change at this temperature? Describe what happens to the initial system, where the reactants and products are in standard states, as it approaches equilibrium.
Solution
The standard free energy change is >When reactants and products are in their standard states (1 bar or 1 atm), Q = 1. As the reaction proceeds toward equilibrium, the reaction shifts left (the amount of products drops while the amount of reactants increases): Q < 1, and becomes less positive as it approaches zero. At equilibrium, Q = K, and ΔG = 0.
Determine the normal boiling point (in kelvin) of dichloromethane, CH2Cl2. Find the actual boiling point using the Internet or some other source, and calculate the percent error in the temperature. Explain the differences, if any, between the two values.
Under what conditions is spontaneous?
Solution
The reaction will be spontaneous at temperatures greater than 287 K.
At room temperature, the equilibrium constant (Kw) for the self-ionization of water is 1.00 10−14. Using this information, calculate the standard free energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce water. (Hint: The reaction is the reverse of the self-ionization reaction.)
Hydrogen sulfide is a pollutant found in natural gas. Following its removal, it is converted to sulfur by the reaction
What is the equilibrium constant for this reaction? Is the reaction endothermic or exothermic?
Solution
K = 5.35
1015;
The process is exothermic.
Consider the decomposition of CaCO3(s) into CaO(s) and CO2(g). What is the equilibrium partial pressure of CO2 at room temperature?
In the laboratory, hydrogen chloride (HCl(g)) and ammonia (NH3(g)) often escape from bottles of their solutions and react to form the ammonium chloride (NH4Cl(s)), the white glaze often seen on glassware. Assuming that the number of moles of each gas that escapes into the room is the same, what is the maximum partial pressure of HCl and NH3 in the laboratory at room temperature? (Hint: The partial pressures will be equal and are at their maximum value when at equilibrium.)
Solution
1.0 10−8 atm. This is the maximum pressure of the gases under the stated conditions.
Benzene can be prepared from acetylene.
Determine the equilibrium constant at 25 °C and at 850 °C. Is the reaction spontaneous at either of these temperatures? Why is all acetylene not found as benzene?
Carbon dioxide decomposes into CO and O2 at elevated temperatures. What is the equilibrium partial pressure of oxygen in a sample at 1000 °C for which the initial pressure of CO2 was 1.15 atm?
Solution
Carbon tetrachloride, an important industrial solvent, is prepared by the chlorination of methane at 850 K.
What is the equilibrium constant for the reaction at 850 K? Would the reaction vessel need to be heated or cooled to keep the temperature of the reaction constant?
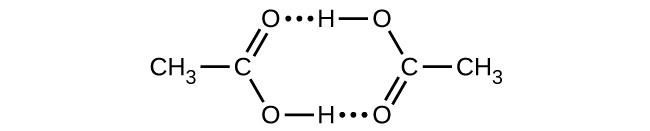
Acetic acid, CH3CO2H, can form a dimer, (CH3CO2H)2, in the gas phase.
The dimer is held together by two hydrogen bonds with a total strength of 66.5 kJ per mole of dimer.