Objectives:
- State the first law of thermodynamics
- Define enthalpy and explain its classification as a state function
- Write and balance thermochemical equations
- Calculate enthalpy changes for various chemical reactions
- Explain Hess’s law and use it to compute reaction enthalpies
Thermochemistry is a branch of chemical thermodynamics, the science that deals with the relationships between heat, work, and other forms of energy in the context of chemical and physical processes. As we concentrate on thermochemistry in this chapter, we need to consider some widely used concepts of thermodynamics.
Substances act as reservoirs of energy, meaning that energy can be added to them or removed from them. Energy is stored in a substance when the kinetic energy of its atoms or molecules is raised. The greater kinetic energy may be in the form of increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy is lost, the intensities of these motions decrease and the kinetic energy falls. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E.
As a system undergoes a change, its internal energy can change, and energy can be transferred from the system to the surroundings, or from the surroundings to the system. Energy is transferred into a system when it absorbs heat (q) from the surroundings or when the surroundings do work (w) on the system. For example, energy is transferred into room-temperature metal wire if it is immersed in hot water (the wire absorbs heat from the water), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature. Conversely, energy is transferred out of a system when heat is lost from the system, or when the system does work on the surroundings.
The relationship between internal energy, heat, and work can be represented by the equation:
$$ΔU=q+w$$This is one version of the first law of thermodynamics, and it shows that the internal energy of a system changes through heat flow into or out of the system (positive q is heat flow in; negative q is heat flow out) or work done on or by the system. The work, w, is positive if it is done on the system and negative if it is done by the system.
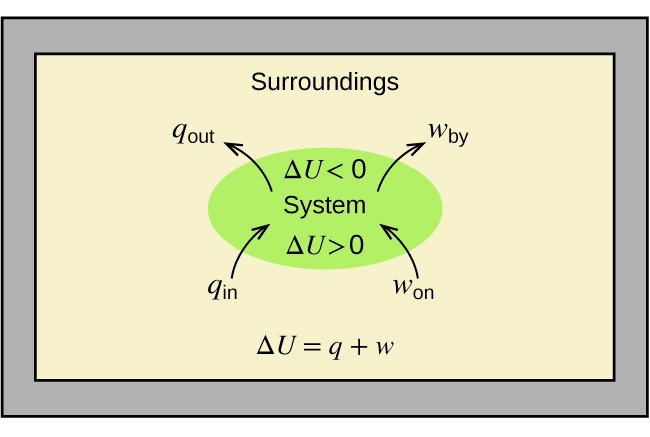
A type of work called expansion work (or pressure-volume work) occurs when a system pushes back the surroundings against a restraining pressure, or when the surroundings compress the system. An example of this occurs during the operation of an internal combustion engine. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, and the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. (The engine is able to keep the car moving because this process is repeated many times per second while the engine is running.) We will consider how to determine the amount of work involved in a chemical or physical change in the chapter on thermodynamics.
This view of an internal combustion engine illustrates the conversion of energy produced by the exothermic combustion reaction of a fuel such as gasoline into energy of motion.
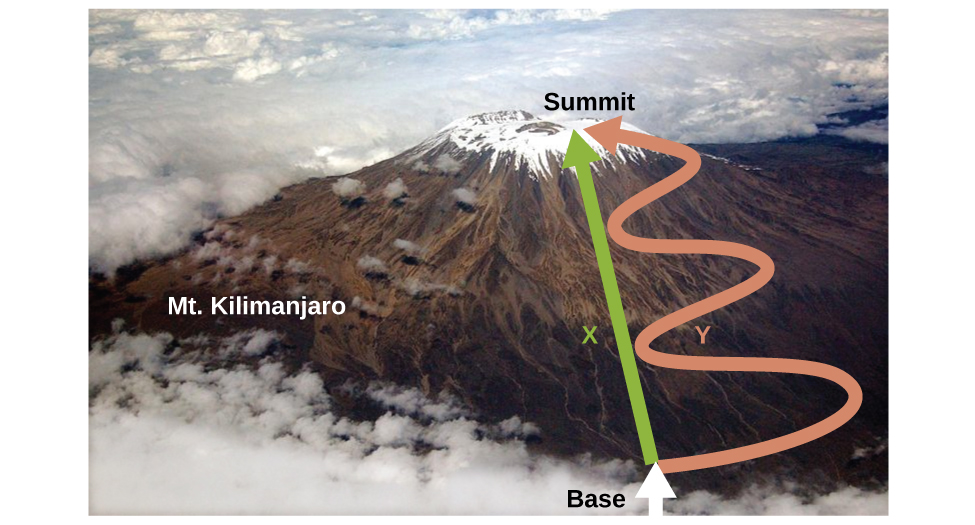
As discussed, the relationship between internal energy, heat, and work can be represented as ΔU = q + w. Internal energy is an example of a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you traveled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path (as seen in the image below). The distances traveled would differ (distance is not a state function) but the elevation reached would be the same (altitude is a state function).
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is defined as the sum of a system’s internal energy (U) and the mathematical product of its pressure (P) and volume (V):
$$H=U+PV$$Enthalpy is also a state function. Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (ΔH) is:
$$ΔH=ΔU+PΔV$$The mathematical product PΔV represents work (w), namely, expansion or pressure-volume work as noted. By their definitions, the arithmetic signs of ΔV and w will always be opposite:
$$PΔV=−w$$Substituting this equation and the definition of internal energy into the enthalpy-change equation yields:
| $ΔH$ | $=ΔU+PΔV$ |
| $=q_p+w-w$ | |
| =$q_p$ |
where qp is the heat of reaction under conditions of constant pressure.
And so, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (qp) and enthalpy change (ΔH) for the process are equal.
The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter (seen on the calorimetry page) is not equal to ΔH because the closed, constant-volume metal container prevents the pressure from remaining constant (it may increase or decrease if the reaction yields increased or decreased amounts of gaseous species). Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with q = ΔH, which makes enthalpy the most convenient choice for determining heat changes for chemical reactions.
The following conventions apply when using ΔH:
- A negative value of an enthalpy change, ΔH < 0, indicates an exothermic reaction; a positive value, ΔH > 0, indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
- Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example, consider this equation: $$H_2\;(g)+\frac{1}{2}O_2\;(g)⟶H_2O\;(l)\qquad ΔH=−286\;kJ/mol$$
This equation indicates that when 1 mole of hydrogen gas and $\frac{1}{2}$ mole of oxygen gas at some temperature and pressure change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor ($ΔH$ is an extensive property):
(two-fold increase in amounts) $2H_2\;(g)+O_2\;(g)⟶2H_2O\;(l)\qquad ΔH=2\times (-286\;kJ)=-572 kJ$ (two-fold decrease in amounts) $\frac{1}{2}H_2\;(g)+\frac{1}{4}O_2\;(g)⟶\frac{1}{2}H_2O\;(l)\qquad ΔH=\frac{1}{2}\times (-286\;kJ)=-143 kJ$ -
The enthalpy change of a reaction depends on the physical states of the reactants and products, so these must be shown. For example, when 1 mole of hydrogen gas and $\frac{1}{2}$ mole of oxygen gas change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released. If gaseous water forms, only 242 kJ of heat are released. $$H_2\;(g)+\frac{1}{2}O_2\;(g)⟶2H_2O\;(g)\qquad ΔH=242\;kJ/mol$$
Writing Thermochemical EquationsWhen 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ of heat are produced.
Write a balanced thermochemical equation for the reaction of one mole of HCl.?
$$HCl\;(aq)+NaOH\;(aq)⟶NaCl\;(aq)+H_2O\;(l)$$Solution
For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. The reactants are provided in stoichiometric amounts (same molar ratio as in the balanced equation), and so the amount of acid may be used to calculate a molar enthalpy change. Since ΔH is an extensive property, it is proportional to the amount of acid neutralized:
The thermochemical equation is then
$$HCl\;(aq)+NaOH\;(aq)⟶NaCl\;(aq)+H_2O\;(l)\qquad ΔH=-58\;kJ$$Check Your Learning
When 1.34 g Zn(s) reacts with 60.0 mL of 0.750 M HCl(aq), 3.14 kJ of heat are produced. Determine the enthalpy change per mole of zinc reacting for the reaction:
Answer:
ΔH = −153 kJ
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.
Writing Thermochemical Equations
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ of heat are produced. Write a thermochemical equation for the reaction of one mole of sucrose:
Solution
Unlike the previous example exercise, this one does not involve the reaction of stoichiometric amounts of reactants, and so the limiting reactant must be identified (it limits the yield of the reaction and the amount of thermal energy produced or consumed).
The provided amounts of the two reactants are $$(2.67\;g)(\frac{1\;mol}{342.3\;g})=0.00780\;mol\;C_{12}H_{22}O_{11}$$ $$(7.19\;g)(\frac{1\;mol}{122.5\;g})=0.0587\;mol\;KClO_3$$
The provided molar ratio of perchlorate-to-sucrose is then
$$\frac{0.0587\;mol\;KClO_3}{0.00780\;mol\;C_{12}H_{22}O_{11}}=7.52$$The balanced equation indicates 8 mol KClO3 are required for reaction with 1 mol C12H22O11. Since the provided amount of KClO3 is less than the stoichiometric amount, it is the limiting reactant and may be used to compute the enthalpy change:
$$\Delta H=\frac{-43.7\;kJ}{0.0587\;mol\;KClO_3}=744\;kJ/mol\;KClO_3$$Because the equation, as written, represents the reaction of 8 mol KClO3, the enthalpy change is: (744\;kJ/molKClO_3)(8\;mol\;ClO_3)=5960\;kJ$$
The enthalpy change for this reaction is −5960 kJ, and the thermochemical equation is:
$$C_{12}H_{22}O_{11}\;(aq)+8KClO_3\;(aq)⟶12CO_2\;(g)+11H_2O\;(l)+8KCl(aq)\qquad ΔH=-5960\;kJ/mol$$Check Your Learning
When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl2(s) and 8.60 kJ of heat is produced. What is the enthalpy change for the reaction when 1 mole of FeCl2(s) is produced?
Answer:
ΔH = −338 kJ