Variation in Covalent Radii - UCalgary Chemistry Textbook

The quantum mechanical picture makes it difficult to establish a definite size of an atom. However, there are several practical ways to define the radius of atoms and, thus, to determine their relative sizes that give roughly similar values. We will use the covalent radius, which is defined as one-half the distance between the nuclei of two identical atoms when they are joined by a covalent bond (this measurement is possible because atoms within molecules still retain much of their atomic identity).

The radius of an atom is defined as one-half the distance between the nuclei in a molecule consisting of two identical atoms joined by a covalent bond. The atomic radius for the halogens increases down the group as n increases.

Going down a group:

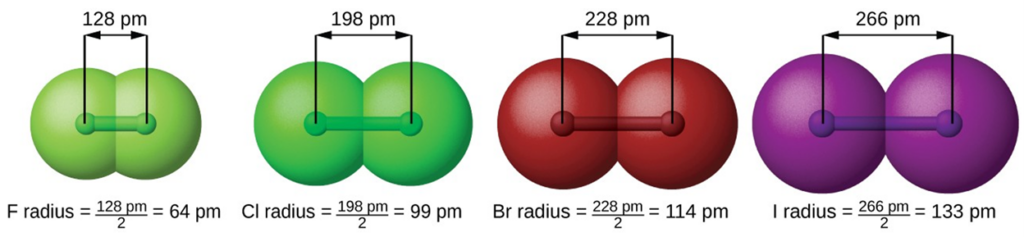
We know that as we scan down a group, the principal quantum number, n, increases by one for each element. Thus, the electrons are being added to a region of space that is increasingly distant from the nucleus. Consequently, the size of the atom (and its covalent radius) must increase as we increase the distance of the outermost electrons from the nucleus. This trend is illustrated for the covalent radii of the halogens in the table and figure below. The trends for the entire periodic table can be seen in the periodic table picture below.

Atom	Covalent radius (pm)	Nuclear charge
F	64	+9
Cl	99	+17
Br	114	+35
I	133	+53
At	148	+85

Covalent radii of the elements are shown to scale. The general trend is that radii increase down a group and decrease across a period.

Going across a period:

As shown in Figure 2 above and Figure 3 below, as we move across a period from left to right, we generally find that each element has a smaller covalent radius than the element preceding it. This might seem counterintuitive because it implies that atoms with more electrons have a smaller atomic radius.

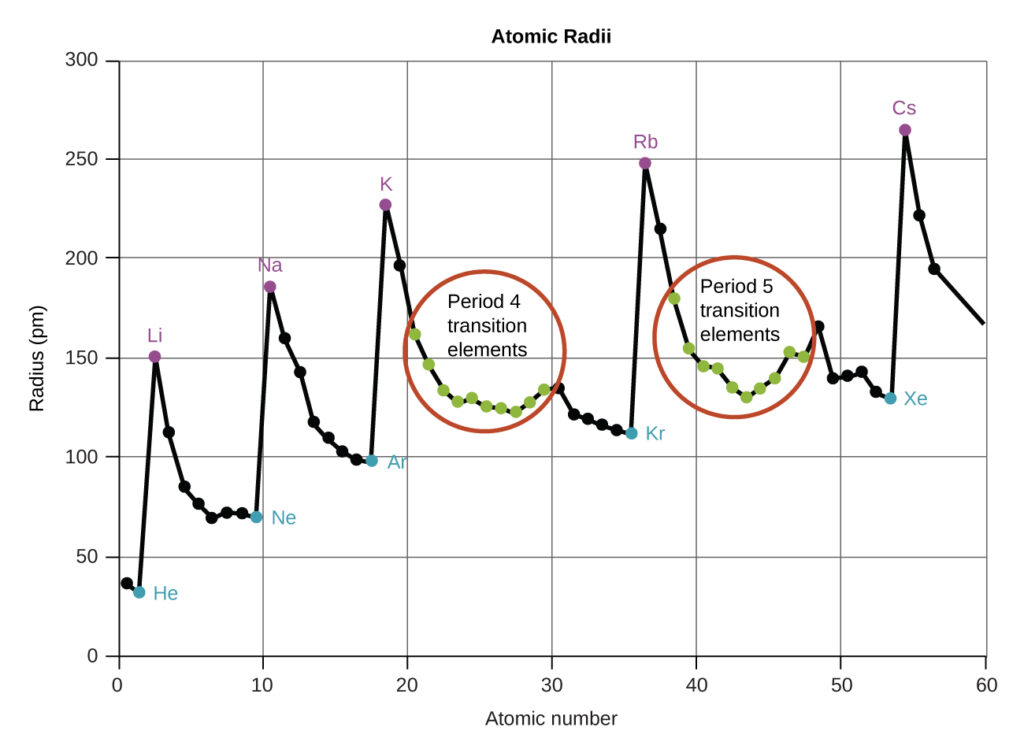
Within each period, the trend in atomic radius decreases as Z increases; for example, from K to Kr. Within each group (e.g., the alkali metals shown in purple), the trend is that atomic radius increases as Z increases.

This can be explained with the concept of effective nuclear charge, Z_eff, each time we move from one element to the next across a period, Z increases by one, but the shielding increases only slightly. Thus, Z_eff increases as we move from left to right across a period. The stronger pull (higher effective nuclear charge) experienced by electrons on the right side of the periodic table draws them closer to the nucleus, making the covalent radii smaller.

Sorting Atomic Radii
Predict the order of increasing covalent radius for Ge, Fl, Br, Kr.

Solution
Radius increases as we move down a group, so Ge < Fl (Note: Fl is the symbol for flerovium, element 114, NOT fluorine).

Radius decreases as we move across a period, so Kr < Br < Ge. Putting the trends together, we obtain Kr < Br < Ge < Fl.