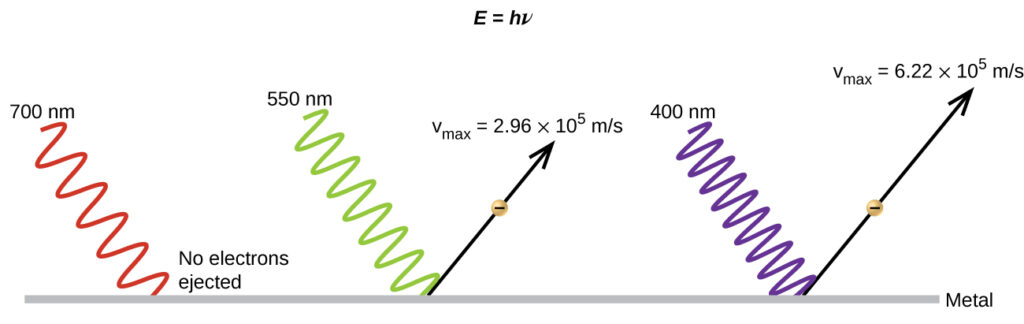
The next paradox in the classical theory concerned the photoelectric effect. Scientist observed that shining light with a frequency greater than a certain threshold frequency on a clean metal surface, could eject electrons from it. Surprisingly, the kinetic energy of the ejected electrons did not depend on the brightness of the light. Instead, the kinetic energy increased with increasing frequency of the light. To eject the electrons, they need more energy due to certain amount of energy keeping them bound to the metal. Therefore, the incident light energy needed to be greater in order to free the electrons.
Einstein’s Solution
According to classical wave theory, a wave’s energy depends on its intensity (which depends on its amplitude), not its frequency. One part of these observations was that the number of electrons ejected increased as the brightness increased. In 1905, Albert Einstein resolved the paradox by incorporating Planck’s quantization findings into the discredited particle view of light. Interestingly, Einstein actually won his Nobel prize for this work, not for his theories of relativity.
Quantum Explanation
Einstein argued that the quantized energies, as postulated by Planck in his treatment of blackbody radiation, could be extended to explain the photoelectric effect. Acoording to Plank, it is stated that light striking the metal surface should not be viewed as a wave, but as a stream of particles (later called photons). The energy of these particles (photons) depended on their frequency, according to Planck’s formula, $E=hν$ (or, in terms of wavelength using $c=νλ$, $E=\frac{hc}{λ}$). Electrons ejected when hit by photons with sufficient energy (a frequency greater than the threshold). The greater the frequency, the greater the kinetic energy imparted to the escaping electrons by the collisions.
Einstein also argued that the light intensity did not depend on the amplitude of the incoming wave, but instead corresponded to the number of photons striking the surface within a given time period. This explains why the number of ejected electrons increased with increasing brightness. The greater the number of incoming photons, the greater the likelihood that they would collide with some of the electrons.
Wave-Particle Duality
With Einstein’s findings, the nature of light took on a new air of mystery: the light phenomena. The light phenomena states that light could be either a waves or particles, and you may ask why this is. Well, certain phenomena, such as the interference patterns, light passed through a double slit, is completely contrary to a particle view of light. In contrast, other phenomena, such as the photoelectric effect, were completely contrary to a wave view of light. Somehow, at a deep fundamental level, light is still not fully understood. So, scientist came up with a an explanation that would satisfy both phenomena; wave-particle duality, light is both wavelike and particle-like.
Calculating the Energy of Radiation
When we see light from a neon sign, we are observing radiation from excited neon atoms. If this radiation has a wavelength of 640 nm, what is the energy of the photon being emitted?
Solution
We use the part of Planck’s equation that includes the wavelength, λ, and convert units of nanometers to meters so that the units of λ and c are the same.
$$E=\frac{hc}{ λ }$$
$$E=\frac{(6.626×10^{-34}\;J\require{enclose}\enclose{horizontalstrike}{s})(2.998×10^8\;m\enclose{horizontalstrike}{s^{-1}})}{(640\;nm)(\frac{1\;m}{10^9\;\enclose{horizontalstrike}{nm}})}$$
$$E=3.10×10^{-19}\;J$$
Check Your Learning
The microwaves in an oven are of a specific frequency that will heat the water molecules contained in food. (This is why most plastics and glass do not become hot in a microwave oven-they do not contain water molecules.) This frequency is about 3 × 109 Hz. What is the energy of one photon in these microwaves?
Answer:
2 × 10−24 J
Use this simulation program to experiment with the photoelectric effect to see how intensity, frequency, type of metal, and other factors influence the ejected photons:
This link will open the CheerpJ compatible app, which can sometimes load slowly. At the link above, you can download the full Java version.
Example: Photoelectric Effect
Identify which of the following statements are false and, where necessary, change the italicized word or phrase to make them true, consistent with Einstein’s explanation of the photoelectric effect.
(a) Increasing the brightness of incoming light increases the kinetic energy of the ejected electrons.
(b) Increasing the wavelength of incoming light increases the kinetic energy of the ejected electrons.
(c) Increasing the brightness of incoming light increases the number of ejected electrons.
(d) Increasing the frequency of incoming light can increase the number of ejected electrons.
Solution
(a) False. Increasing the brightness of incoming light has no effect on the kinetic energy of the ejected electrons. Only energy, not the number or amplitude, of the photons influences the kinetic energy of the electrons.
(b) False. Increasing the frequency of incoming light increases the kinetic energy of the ejected electrons. Frequency is proportional to energy and inversely proportional to wavelength. Frequencies above the threshold value transfer the excess energy into the kinetic energy of the electrons.
(c) True. Because the number of collisions with photons increases with brighter light, the number of ejected electrons increases.
(d) True with regard to the threshold energy binding the electrons to the metal. Below this threshold, electrons are not emitted and above it they are. Once over the threshold value, further increasing the frequency does not increase the number of ejected electrons
Check Your Learning
Calculate the threshold energy in kJ/mol of electrons in aluminum, given that the lowest frequency photon for which the photoelectric effect is observed is 9.87 × 1014 Hz.
Answer:
394 kJ/mol