A bond’s strength indicates how strongly each atom connects with another. It also shows how much energy is needed to break the bond between them. In this section, you will learn about the bond strength of covalent bonds. Then, you will compare this to the strength of ionic bonds, which relates to the lattice energy of a compound.
Bond Strength: Covalent Bonds
Stable molecules exist because covalent bonds hold the atoms together. We measure the strength of a covalent bond by the energy required to break it, that is, the energy necessary to separate the bonded atoms. Separating any pair of bonded atoms requires energy. The stronger a bond, the greater the energy required to break it.
We call the energy required to break a specific covalent bond in one mole of gaseous molecules the bond energy or bond dissociation energy. The bond energy for a diatomic molecule, DX–Y, is defined as the standard enthalpy change for the endothermic reaction: $$XY(g)⟶X\;(g)+Y\;(g)\qquad D_{X−Y}=ΔH°$$
For example, the bond energy of the pure covalent H–H bond, DH–H, is 436 kJ per mole of H–H bonds broken: $$H_2(g)⟶2H(g)\qquad D_{H−H}=ΔH°=436\;kJ/mol$$
Multiple Bond Energies
Molecules with three or more atoms have two or more bonds. The sum of all bond energies in such a molecule equals the standard enthalpy change for the reaction. This reaction is endothermic and involves breaking all the bonds in the molecule. For example, the sum of the four C–H bond energies in CH4, 1660 kJ, is equal to the standard enthalpy change of the reaction:
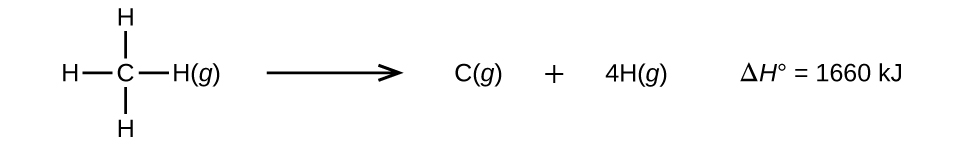
The average C–H bond energy, DC–H, is calculated as 1660/4 = 415 kJ/mol because the reaction breaks four moles of C–H bonds per mole. Although the four C–H bonds are equivalent in the original molecule, breaking each bond requires different amounts of energy. Breaking the first bond requires 439 kJ/mol, and the remaining bonds are easier to break. The 415 kJ/mol value is the average, not the exact value required to break any one bond.
The strength of a bond between two atoms increases as the number of electron pairs in the bond increases. Generally, as the bond strength increases, the bond length decreases. Thus, we find that triple bonds are stronger and shorter than double bonds between the same two atoms. Similarly, double bonds are stronger and shorter than single bonds between the same two atoms.
Average bond energies for some common bonds appear in the Table 1 below. A comparison of bond lengths and bond strengths for some common bonds appears in Table 2 below.
When one atom bonds to various atoms in a group, the bond strength typically decreases as we move down the group. For example, C–F is 439 kJ/mol, C–Cl is 330 kJ/mol, and C–Br is 275 kJ/mol.
Bond Energies kJ/mol
| Bond | Bond Energy | Bond | Bond Energy | Bond | Bond Energy |
|---|---|---|---|---|---|
| H–H | 436 | C–S | 260 | F–Cl | 255 |
| H–C | 415 | C–Cl | 330 | F–Br | 235 |
| H–N | 390 | C–Br | 275 | Si–Si | 230 |
| H–O | 464 | C–I | 240 | Si–P | 215 |
| H–F | 569 | N–N | 160 | Si–S | 225 |
| H–Si | 395 | N=N | 418 | Si–Cl | 359 |
| H–P | 320 | N≡N | 946 | Si–Br | 290 |
| H–S | 340 | N–O | 200 | Si–I | 215 |
| H–Cl | 432 | N–F | 270 | P–P | 215 |
| H–Br | 370 | N–P | 210 | P–S | 230 |
| H–I | 295 | N–Cl | 200 | P–Cl | 330 |
| C–C | 345 | N–Br | 245 | P–Br | 270 |
| C=C | 611 | O–O | 140 | P–I | 215 |
| C≡C | 837 | O=O | 498 | S–S | 215 |
| C–N | 290 | O–F | 160 | S–Cl | 250 |
| C=N | 615 | O–Si | 370 | S–Br | 215 |
| C≡N | 891 | O–P | 350 | Cl–Cl | 243 |
| C–O | 350 | O–Cl | 205 | Cl–Br | 220 |
| C=O | 741 | O–I | 200 | Cl–I | 210 |
| C≡O | 1080 | F–F | 160 | Br–Br | 190 |
| C–F | 439 | F–Si | 540 | Br–I | 180 |
| C–Si | 360 | F–P | 489 | I–I | 150 |
| C–P | 265 | F–S | 285 |
Average Bond Lengths and Bond Energies for Some Common Bonds
| Bond | Bond Length (Å) | Bond Energy (kJ/mol) |
|---|---|---|
| C–C | 1.54 | 345 |
| C=C | 1.34 | 611 |
| C≡C | 1.20 | 837 |
| C–N | 1.43 | 290 |
| C=N | 1.38 | 615 |
| C≡N | 1.16 | 891 |
| C–O | 1.43 | 350 |
| C=O | 1.23 | 741 |
| C≡O | 1.13 | 1080 |
We can use bond energies to calculate approximate enthalpy changes for reactions where enthalpies of formation are not available. Calculations of this type will also tell us whether a reaction is exothermic or endothermic. An exothermic reaction (ΔH negative, heat produced) results when the bonds in the products are stronger than the bonds in the reactants. An endothermic reaction (ΔH positive, heat absorbed) results when the bonds in the products are weaker than those in the reactants.
Ionic Bond Strength and Lattice Energy
An ionic compound is stable because of the electrostatic attraction between its positive and negative ions. The lattice energy of a compound is a measure of the strength of this attraction. The lattice energy (ΔHlattice) of an ionic compound is the energy required to separate one mole of the solid into its component gaseous ions. For the ionic solid MX, the lattice energy is the enthalpy change of the process:
$$MX\;(s)⟶Mn^+(g)+Xn^−(g)\qquad ΔH_{lattice}$$
The bond dissociation energy measures the strength of a covalent bond. It represents the amount of energy required to break that particular bond in a mole of molecules. . Multiple bonds are stronger than single bonds between the same atoms.
Chemistry End of Chapter Exercises
Which bond in each of the following pairs of bonds is the strongest?
(a) C–C or C=C
(b) C–N or C≡N
(c) C≡O or C=O
(d) H–F or H–Cl
(e) C–H or O–H
(f) C–N or C–O