By the end of this section, you will be able to:
- Describe and relate the definitions of electrode and cell potentials
- Interpret electrode potentials in terms of relative oxidant and reductant strengths
- Calculate cell potentials and predict redox spontaneity using standard electrode potentials
Unlike the spontaneous oxidation of copper by aqueous silver(I) ions described in the previous section, immersing a copper wire in an aqueous solution of lead(II) ions yields no reaction. The two species, Ag+(aq) and Pb2+(aq), thus show a distinct difference in their redox activity towards copper: the silver ion spontaneously oxidized copper, but the lead ion did not. Electrochemical cells permit this relative redox activity to be quantified by an easily measured property, potential. This property is more commonly called voltage when referenced in regard to electrical applications, and it is a measure of energy accompanying the transfer of charge. Potentials are measured in the volt unit, defined as one joule of energy per one coulomb of charge, V = J/C.
When measured for purposes of electrochemistry, a potential reflects the driving force for a specific type of charge transfer process, namely, the transfer of electrons between redox reactants. Considering the nature of potential in this context, it is clear that the potential of a single half-cell or a single electrode can’t be measured; “transfer” of electrons requires both a donor and recipient, in this case a reductant and an oxidant, respectively. Instead, a half-cell potential may only be assessed relative to that of another half-cell. It is only the difference in potential between two half-cells that may be measured, and these measured potentials are called cell potentials, Ecell, defined as
$$E_{cell}=E_{cathode}-E_{anode}$$where Ecathode and Eanode are the potentials of two different half-cells functioning as specified in the subscripts. As for other thermodynamic quantities, the standard cell potential, E°cell, is a cell potential measured when both half-cells are under standard-state conditions (1 M concentrations, 1 bar pressures, 298 K):
$$E^°_{cell}=E^°_{cathode}-E^°_{anode}$$To simplify the collection and sharing of potential data for half-reactions, the scientific community has designated one particular half-cell to serve as a universal reference for cell potential measurements, assigning it a potential of exactly 0 V. This half-cell is the standard hydrogen electrode (SHE) and it is based on half-reaction below:
$$2H^+(aq)+2e^-⟶H_2(g)$$A typical SHE contains an inert platinum electrode immersed in precisely 1 M aqueous H+ and a stream of bubbling H2 gas at 1 bar pressure, all maintained at a temperature of 298 K.
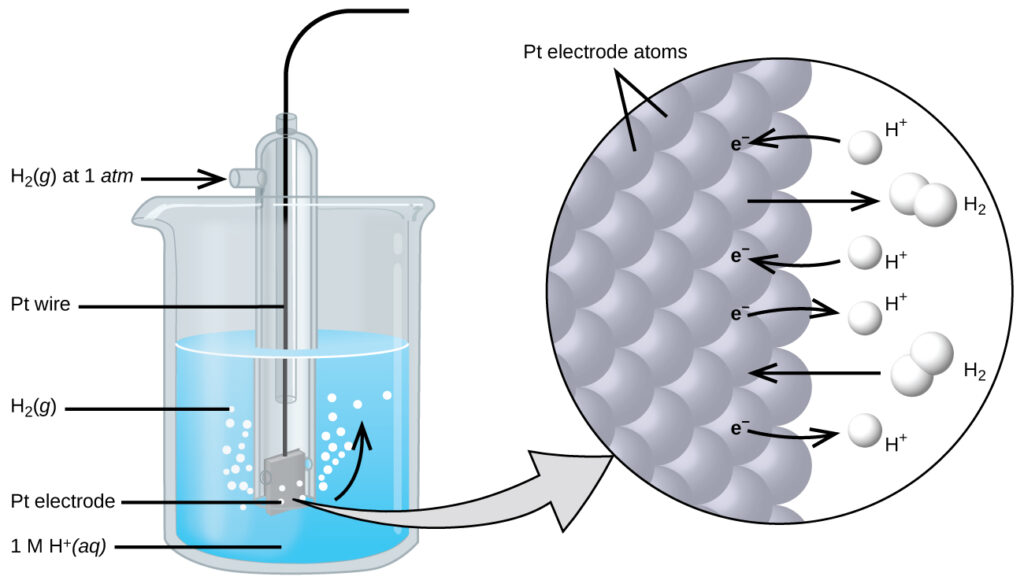
The assigned potential of the SHE permits the definition of a conveniently measured potential for a single half-cell. The electrode potential (EX) for a half-cell X is defined as the potential measured for a cell comprised of X acting as cathode and the SHE acting as anode:
$$E_{cell}=E_{\text{X}}-E_{\text{SHE}}$$ $$E_{\text{SHE}}=0\;V\;\text{(defined)}$$ $$E_{cell}=E_{\text{X}}$$When the half-cell X is under standard-state conditions, its potential is the standard electrode potential, E°X. Since the definition of cell potential requires the half-cells function as cathodes, these potentials are sometimes called standard reduction potentials.
This approach to measuring electrode potentials is illustrated in the figure below, which depicts a cell comprised of an SHE connected to a copper(II)/copper(0) half-cell under standard-state conditions. A voltmeter in the external circuit allows measurement of the potential difference between the two half-cells. Since the Cu half-cell is designated as the cathode in the definition of cell potential, it is connected to the red (positive) input of the voltmeter, while the designated SHE anode is connected to the black (negative) input. These connections insure that the sign of the measured potential will be consistent with the sign conventions of electrochemistry per the various definitions discussed above. A cell potential of +0.337 V is measured, and so
$$E^°_{cell}=E^°_{Cu}=+0.337\;V$$Tabulations of E° values for other half-cells measured in a similar fashion are available as reference literature to permit calculations of cell potentials and the prediction of the spontaneity of redox processes.

$$Cu^{2+}(aq)+2e^-⟶Cu(s)$$
The table below provides a listing of standard electrode potentials for a selection of half-reactions in numerical order, and a more extensive alphabetical listing is given in the Appendix.
| Half-Reaction | E° (V) | |
|---|---|---|
| $F_2(g)+2e^-⟶2F^-(aq)$ | +2.866 | |
| $PbO_2(s)+SO_4^{2-}(aq)+4H^+(aq)+2e^-⟶PbSO_4(s)+2H_2O(l)$ | +1.69 | |
| $MnO_4^-(aq)+8H^+(aq)+5e^-⟶Mn^{2+}(aq)+4H_2O(l)$ | +1.507 | |
| $Au^{3+}(aq)+3e^-⟶Au(s)$ | +1.498 | |
| $Cl_2(g)+2e^-⟶2Cl^-(aq)$ | +1.35827 | |
| $O_2(g)+4H^+(aq)+4e^-⟶2H_2O(l)$ | +1.229 | |
| $Pt^{2+}(aq)+2e^-⟶Pt(s)$ | +1.20 | |
| $Br_2(aq)+2e^-⟶2Br^-(aq)$ | +1.0873 | |
| $Ag^+(aq)+e^-⟶Ag(s)$ | +0.7996 | |
| $Hg_2^{2+}(aq)+2e^-⟶2Hg(l)$ | +0.7973 | |
| $Fe^{3+}(aq)+e^-⟶Fe^{2+}(aq)$ | +0.771 | |
| $MnO_4^-(aq)+2H_2O(l)+3e^-⟶MnO_2(s)+4OH^-(aq)$ | +0.558 | |
| $I_2(s)+2e^-⟶2I^-(aq)$ | +0.5355 | |
| $NiO_2(s)+2H_2O(l)+2e^-⟶Ni(OH)_2(s)+2OH^-(aq)$ | +0.49 | |
| $Cu^{2+}(aq)+2e^-⟶Cu(s)$ | +0.34 | |
| $Hg_2Cl_2(s)+2e^-⟶2Hg(l)+2Cl^-(aq)$ | +0.26808 | |
| $AgCl(s)+e^-⟶Ag(s)+Cl^-(aq)$ | +0.22233 | |
| $Sn^{4+}(aq)+2e^-⟶Sn^{2+}(aq)$ | +0.151 | |
| $2H^+(aq)+2e^-⟶H_2(g)$ | 0.00 | |
| $Pb^{2+}(aq)+2e^-⟶Pb(s)$ | −0.1262 | |
| $Sn^{2+}(aq)+2e^-⟶Sn(s)$ | −0.1375 | |
| $Ni^{2+}(aq)+2e^-⟶Ni(s)$ | −0.257 | |
| $Co^{2+}(aq)+2e^-⟶Co(s)$ | −0.28 | |
| $PbSO_4(s)+2e^-⟶Pb(s)+SO_4^{2-}(aq)$ | −0.3505 | |
| $Cd^{2+}(aq)+2e^-⟶Cd(s)$ | −0.4030 | |
| $Fe^{2+}(aq)+2e^-⟶Fe(s)$ | −0.447 | |
| $Cr^{3+}(aq)+3e^-⟶Cr(s)$ | −0.744 | |
| $Mn^{2+}(aq)+2e^-⟶Mn(s)$ | −1.185 | |
| $Zn(OH)_2(s)+2e^-⟶Zn(s)+2OH^-(aq)$ | −1.245 | |
| $Zn^{2+}(aq)+2e^-⟶Zn(s)$ | −0.7618 | |
| $Al^{3+}(aq)+3e^-⟶Al(s)$ | −1.662 | |
| $Mg^{2+}(aq)+2e^-⟶Mg(s)$ | −2.372 | |
| $Na^+(aq)+e^-⟶Na(s)$ | −2.71 | |
| $Ca^{2+}(aq)+2e^-⟶Ca(s)$ | −2.868 | |
| $Ba^{2+}(aq)+2e^-⟶Ba(s)$ | −2.912 | |
| $K^+(aq)+e^-⟶K(s)$ | −2.931 | |
| $Li^+(aq)+e^-⟶Li(s)$ | −3.04 | |
Calculating Standard Cell Potentials
What is the standard potential of the Cu-Ag galvanic cell?
Solution
This cell is galvanic, the spontaneous cell reaction involving oxidation of its copper anode and reduction of silver(I) ions at its silver cathode:
| cell reaction: | $Cu(s)+2Ag^+(aq)⟶Cu^{2+}(aq)+2Ag(s)$ |
| anode half-reaction: | $Cu(s)⟶Cu^{2+}(aq)+2e^-$ |
| cathode half-reaction: | $2Ag^+(aq)+2e^-⟶2Ag(s)$ |
The standard cell potential computed as
$$E^°_{cell}=E^°_{cathode}-E^°_{anode}$$ $$E^°_{cell}=E^°_{Ag}-E^°_{Cu}$$ $$E^°_{cell}=0.7996\;V-0.34\;V$$ $$E^°_{cell}=+0.46\;V$$Check Your Learning
What is the standard cell potential expected if the silver cathode half-cell in the Cu-Ag cell is replaced with a lead half-cell: $Pb^{2+}(aq)+2e^-⟶Pb(s)$?
Answer:
−0. 47 V