Combining a previously derived relation between ΔG° and K (see the chapter on thermodynamics) and the equation above relating ΔG° and E°cell yields the following:
$ ΔG° = −RTlnK = −nFE_{cell}^° $
$ E_{cell}^° = (\frac{RT}{nF})lnK $
This equation indicates redox reactions with large (positive) standard cell potentials will proceed far towards completion, reaching equilibrium when the majority of reactant has been converted to product. A summary of the relations between E°, ΔG° and K is depicted in the figure below, and a table correlating reaction spontaneity to values of these properties is provided underneath.
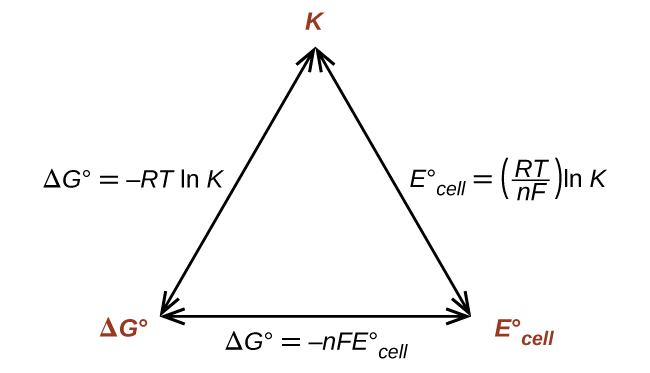
Graphic depicting the relation between three important thermodynamic properties.
| K | ΔG° | E°cell | |
| > 1 | < 0 | > 0 | Reaction is spontaneous under standard conditions Products more abundant at equilibrium |
| < 1 | > 0 | < 0 | Reaction is non-spontaneous under standard conditions Reactants more abundant at equilibrium |
| = 1 | = 0 | = 0 | Reaction is at equilibrium under standard conditions Reactants and products equally abundant |
Equilibrium Constants, Standard Cell Potentials, and Standard Free Energy Changes
Use data from the Appendix to calculate the standard cell potential, standard free energy change, and equilibrium constant for the following reaction at 25 °C. Comment on the spontaneity of the forward reaction and the composition of an equilibrium mixture of reactants and products.
$ 2 Ag^+(aq) + Fe(s) ⇌ 2Ag(s) + Fe^{2+}(aq)$
Solution
The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using the data in the Appendix.
anode (oxidation): $Fe(s) ⟶ Fe^{2+}(aq) + 2e^− E_{Fe^{2+}/Fe}^°\text{ = −0.447 V}$
cathode (reduction): $2×(Ag^+(aq) + e^− ⟶ Ag(s)) E_{Ag^+/Ag}^°\text{= 0.7996 V}$
$E_{cell}^° = E_{cathode}^° − E_{anode}^° = E_{Ag^+/Ag}^° − E_{Fe^{2+}/Fe}^° \text{= +1.247 V}$
With n = 2, the equilibrium constant is then
$$E_{cell}^° = \frac{\text{0.0592 V}}{n}\text{log K}$$
$$K = 10^{\text{n × }E_{cell}^°\text{/0.0592 V}}$$
$$K = 10^{\text{2 × 1.247 V/0.0592 V}}$$
$$K = 10^{42.128}$$
$$K = 1.3 × 10^{42}$$
The standard free energy is then
$$Δ\text{G}° = −\text{nFE}_{cell}^°$$
$$Δ\text{G}° = −2 × 96,485\;\frac{\text{C}}{\text{mol}} × 1.247 \frac{J}{C}\text{ = −240.6 }\frac{kJ}{mol}$$
The reaction is spontaneous, as indicated by a negative free energy change and a positive cell potential. The K value is very large, indicating the reaction proceeds to near completion to yield an equilibrium mixture containing mostly products.
Check Your Learning
What is the standard free energy change and the equilibrium constant for the following reaction at room temperature? Is the reaction spontaneous?
Sn(s) + 2Cu$^{2+}$(aq) ⇌ Sn$^{2+}$(aq) + 2Cu$^+$(aq)
Answer:
Spontaneous; n = 2; E$_{cell}^°$ = +0.291 V; ΔG° = −56.2 $\frac{kJ}{mol}$; K = 6.8 × 109.