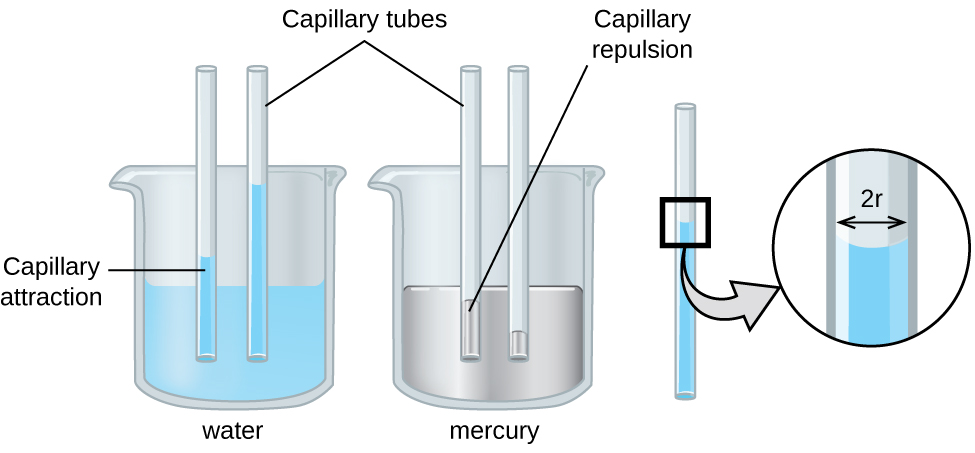
The height to which a liquid will rise in a capillary tube is determined by several factors as shown in the following equation:
$$h\,=\frac{2Tcosθ}{rρg}$$In this equation, h is the height of the liquid inside the capillary tube relative to the surface of the liquid outside the tube, T is the surface tension of the liquid, θ is the contact angle between the liquid and the tube, r is the radius of the tube, ρ is the density of the liquid, and g is the acceleration due to gravity, 9.8 m/s2. When the tube is made of a material to which the liquid molecules are strongly attracted, they will spread out completely on the surface, which corresponds to a contact angle of 0°. This is the situation for water rising in a glass tube.
Capillary Rise
At 25 °C, how high will water rise in a glass capillary tube with an inner diameter of 0.25 mm?
For water, T = 71.99 mN/m and ρ = 1.0 g/cm3.
Solution
The liquid will rise to a height h given by: $h\,=\frac{2Tcosθ}{rρg}$
The Newton is defined as a kg m/s2, and so the provided surface tension is equivalent to 0.07199 kg/s2. The provided density must be converted into units that will cancel appropriately: ρ = 1000 kg/m3. The diameter of the tube in meters is 0.00025 m, so the radius is 0.000125 m. For a glass tube immersed in water, the contact angle is θ = 0°, so cos θ = 1. Finally, acceleration due to gravity on the earth is g = 9.8 m/s2. Substituting these values into the equation, and cancelling units, we have:
$$h\,=\frac{2(0.07199\,kg/s^2)}{(0.000125\,m)(1000\,\frac{kg}{m^3})(9.8\frac{m}{s^2})}=\,0.12\,m\,=\,12\,cm$$
Check Your Learning
Water rises in a glass capillary tube to a height of 8.4 cm. What is the diameter of the capillary tube? Answer:
diameter = 0.36 mm